[改訂/更新情報]
- 2021/07/29: [執筆途中]状態にて公開.
- 2021/11/28: [執筆途中]から,初版執筆完了状態に更新.
記事を通して言いたいこと(結論)
例によって、冒頭で述べておく。
- 飛行機の縦運動と横運動それぞれの状態空間線形時不変計算モデルと,機体フレーム・地上フレームの状態変数を繋げ速度から変位を算出する微分方程式のモデル(オイラー角に関する微分方程式)を組み合わせて,6自由度運動シミュレーションコンポーネントを作成した.
- 文献の付録に記載の,小型飛行機の空力微係数データを使ってシミュレーションを実施したところ,市販のフライトシミュレータで見られるものと似た挙動を確認できる.
モデル化対象(とその周辺について)
縦横分離モデル
表題が示す通り,縦方向(ピッチ回転,x, z軸に沿った加減速)と横方向(ロール,ヨー回転,y軸に沿った加減速)の運動は互いに影響を及ぼし合わないとみなしたモデル.数学的に表現すると,dynamicsの微分方程式が,縦方向の状態変数と横方向の状態変数を繋ぐ項を持たず,互いに独立であるという事になる.ピッチ,ロール,ヨー各方向の回転角・回転加速度が余り大きく無い時に近似できる.
尚,縦と横が交互に作用する項が無いのはdynamicsの微分方程式(力とモーメントの運動方程式)であり,機体フレームと地上フレームの状態変数を関連付けしあうkinamaticsの微分方程式(オイラー角に関する微分方程式)は,縦と横が交互に作用する項を持つ.言い換えると縦と横が独立なのは,機体に働く力とモーメント.
縦系(longitudinal)線形時不変状態空間モデル
この記事にて作成・動作を報告しているので参照されたい.
横系(lateral)線形時不変状態空間モデル
この記事にて作成・動作を報告しているので参照されたい.
kinematics微分方程式:変位算出,機体フレームと地上フレームの状態変数の関連付け
機体フレーム基準の速度,角速度から,地上フレーム基準の位置,姿勢角を算出する非線形微分方程式.ただし,本コンポーネントに実装するのは,6つある方程式のうち,不足している位置を算出する3つのみ.姿勢角についての3つは使わない.上述の線形時不変非線形モデルに,線形化・縦横分離の前提に基づいて簡略化された算出式が入っているので,そのoutuptをそのまま使う.姿勢角についても非線形の方程式を実装した方がより正確なシミュレーションが可能な筈だが,それについては別コンポーネントを作成し,比較する機会を設けるとしよう.
剛体の回転・併進が混ざった,固定フレーム・移動フレームが関わり合う運動は非常に複雑で,解説を書き出すと到底記事1つで収められるものではない.なので当該方程式についての詳しい解説は省略するが,興味を持ってられる方に参考資料を紹介しておく.
コンポーネント
インターフェイスは非常にシンプル.縦系・横系それぞれで機体への制御入力だった,エレベータ,エンジン推力,エルロン,ラダーの操作量(すべて,線形化の基準となる釣り合い状態からの変化量)を入力するreal input connectorのみ.expandable connectorも有しているが,これは飛行状態センサの接続等特別な用途に使うもの.

内部の構成はと言うと,線形縦系コンポーネントの記事と線形横系コンポーネントの記事で作成した動作確認用モデルを1つのモデルに統合し,kinematics微分方程式のコンポーネントを追加して,それを1つのコンポーネントに纏めたものになる.
内部にequationの記述は有るが,その殆どが内部コンポーネント・variable間の接続で,物理的な方程式はほぼ総て内部コンポーネント内で処理している.

シミュレーションモデル
Diagram
動作確認モデルの作りはシンプルそのもの.機体の特性を決めるのは,無次元空力微係数と,有次元化に使う質量や翼面積と言った機体の代表parameterのみ.従ってdiagram上で接続するのは3舵とエンジン推力の操作だけだ.
なお,gなどの定数を格納した”environment”コンポーネントを最上層に置いておかなければならない点は,他のAicraftDynamicsライブラリのコンポーネントを使う際と同様.プログラミング時の”おまじない”のようなもの.

Parameter
普段のModelicaモデルと多少異なり(他の記事で見られるように,多くのModelicaモデルでは各コンポーネントの繋ぎ方,と各コンポーネントに与えるparameterの2つで対象システムの特性が決まる.),本モデルでは機体の運動特性はparameterの無次元空力微係数で決定される.本コンポーネントでは機体の幾何形状・コンフィギュレーションから算出するのではなく,直接与えるようになっているため,どれほど実現し得ない突飛な値でもシミュレーションは出来てしまう.そのため,無次元微係数の設定には慎重を期す必要がある.長さなどを与える場合のような,取り敢えず現実的に有り得そうな適当な値を入れてみるという事ができない.
今回の動作確認では,文献付録に記載の既知の機体の無次元空力微係数および代表parameter(質量など)を入力する.機体はCessna 182で,有名極まる小型飛行機Cessna 172の兄弟機だ.機体の運動特性も性能諸元もピーキーなものは何も無く極めて一般的.また,Cessna 172が殆どすべてのフライトシミュレーションソフトに収録されており,”検証”として挙動を比較するのが容易だ.無次元空力微係数の値を列挙すると膨大な数となるので,値を知りたい方は,例モデルのソースコードを参照されたい.
シミュレーション実行
- Δエレベータ舵角(操縦桿の前後操作): AirplaneDyn.u_deltaE
- Δラダー舵角(ラダーペダルの左右踏み込み操作): AirplaneDyn.u_deltaR
- Δエルロン舵角(操縦桿の左右操作): AirplaneDyn.u_deltaA
- Δ推力(スロットルレバー操作): AirplaneDyn.u_deltaT
- C182搭載エンジンの定格出力, pwrStd= 180 [hp] = 134280 [W]
- 線形化の基準とした平衡定常飛行状態における機速, Vinfi= 67.33 [m/s]
- 巡行時定格推力, TstdCru= pwrStd/Vinfi = 134280/67.33 = 1994 [N]
- ΔT/TstdCru= 472/1994 = 0.24 (24%)
- 平面飛行軌跡: AirplaneDyn.fltStates.xNorth vs. .xEast
- 機首方位角: AirplaneDyn.fltStates.psi
- 飛行高度: AirplaneDyn.fltStates.alt
- 飛行状態角: AirplaneDyn.fltStates.theta, .gamma, .phi, .beta
- 飛行軌跡(3D,Z軸範囲を誇張): AirplaneDyn.fltStates.alt, .xNorth, .xEast
- 飛行軌跡(3D,Z軸を10,000まで表示): AirplaneDyn.fltStates.alt, .xNorth, .xEast
Input
本動作確認では,4つのinputを総て順々に操作して応答を観てゆく.尚,線形化モデルでは,これら入力値は絶対値ではなく,線形化の基準となった平衡定常状態での値からの変化値であることに注意されたい.
ピッチアップさせるよう操縦桿を短時間引いて中立に戻し,少し間を開けたた後,逆にピッチダウンするように押し,またすぐに中立位置に戻すように操作する.上下共に3°動かしている.何度かシミュレーションを行て設定した適当な値なのだが,エレベータの稼働範囲が両方向に20°程度であることを考えると穏やかな舵角操舵だろう.

右舷方向に機首を振らせるよう右ペダルを短時間踏み込んで中立に戻し,少し間を開けた後に逆に左舷方向に機首を振らせるべく左ペダルを踏み込む.右に3°,左に2.8°動かしている.何度かシミュレーションを行て設定した適当な値なのだが,ラダーの稼働範囲が両方向に15°~20°程度であることを考えると穏やかな舵角操舵だろう.

左にロールさせるべく操縦桿を左に短時間倒して中立に戻し,少し間を開けた後に逆に右にロールさせるべく操縦桿を右に倒しすぐに中立位置に戻す.左右共に3.2°動かしている.何度かシミュレーションを行て設定した適当な値なのだが,エルロンの稼働範囲が両方向に20°程度であることを考えると穏やかな舵角操舵だろう.
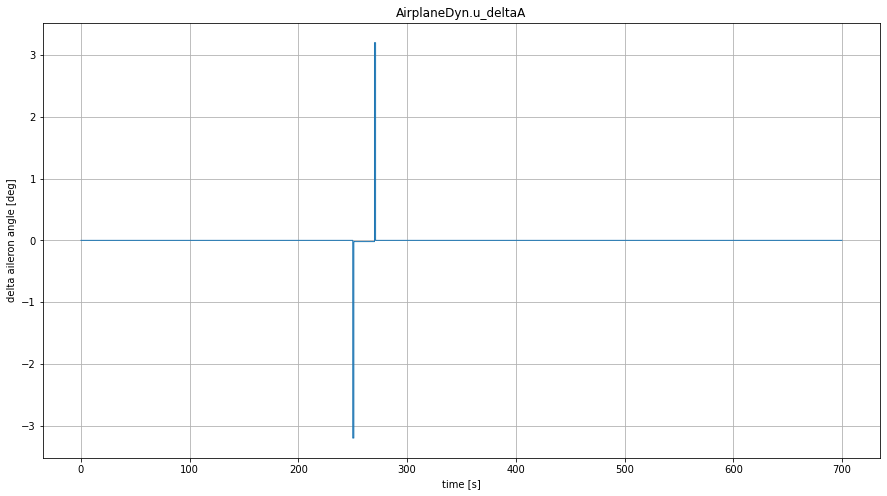
約472 [N] の推力増加を100 [s] 与えている.結果の項でも述べるが,この操作により機は機首上げ姿勢が変化し上昇運動へと転ずる筈である.472 [N] という値は適当に設定したものでは有るが,下記の通り現実的な推力増加操作であることは確認している.
まず,C182のエンジンはレシプロプロペラエンジンであり,推力が飛行速度に応じて異なる(エンジンの出力が飛行速度によらずほぼ一定)ため,”定格推力”というものは無い.なので,操作したΔ推力が,巡行速度における推力に対して,何割程度なのかを簡単に確認する.
*プロペラ効率,出力伝達効率は無視
上記から,定格推力の24%の推力増加操作を行っていることになる.巡行時に最大推力で飛行することは稀で,定格推力の約75%程度にエンジン出力をセットして飛ぶことが一般的である事を考えると,このΔ推力操作はスロットルを巡行状態セットから最大に押し込む操作とほぼ同じであり,現実的な範囲の操作と言える.

Variables
横方向については,時刻100 [s] からののラダー操舵(右舷への首振り)による右旋回と,時刻250 [s] からのエルロン操舵による左旋回を確認できる軌跡となっている.
一般に,飛行機はラダーによる首振りで旋回することは無く,ラダー操舵は横滑りの制御に使うのだが,横滑りに伴って副次的にバンク角変化が生じ,結果としてラダー操舵で旋回が生じている.

値が大きくなる事が右舷方向へ旋回していることを,値が小さくなる(または負値で大きさが大きくなる)事が左舷方向へ旋回している事を示す.ラダー操舵に伴う右旋回と,エルロン操舵に伴う左旋回が確認できる推移となっている.前項のコメントとも繋がる話だが,ラダー操舵による旋回はエルロン操舵による旋回より緩やか(機首方位角変化率が小さい)なものとなっている.

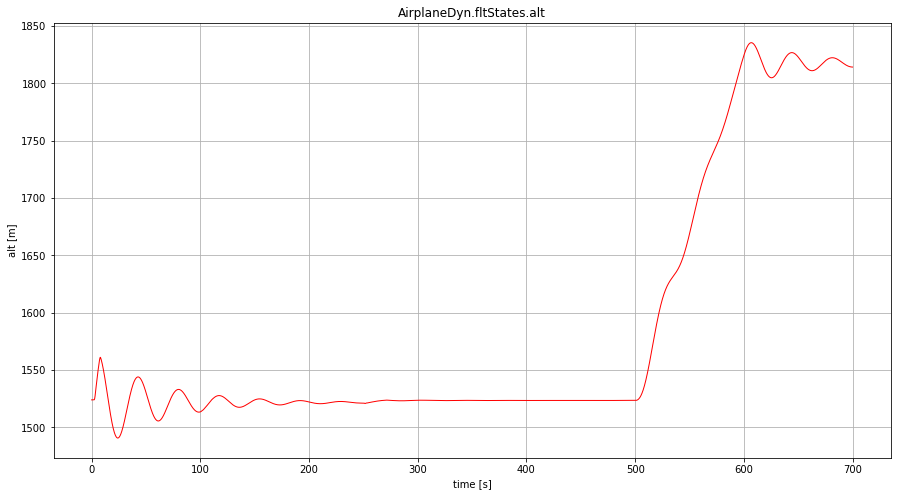
シミュレーション開始直後のエレベータ操作と,時刻500 [s] からのエンジン推力操作に伴う振動が確認できる.どちらも数十秒から100秒オーダーに渡る減衰の小さい動きで,共にフゴイド(長周期)モードの縦振動が飛行高度に現れたものだ.
ここで注目して頂きたいのは,エレベータ操舵では飛行高度がほぼ全く変化せず,エンジン推力を増すと機が上昇している事.次項でピッチ角,鉛直飛行パス角も観て頂くが,エンジン推力だけを増すと,機は勝手に機首を持ち上げて上昇するという事だ(迎角は殆ど変わらない).3D飛行機シューティングゲーム等での飛行機の動きに馴染むと,機首の上げ下げで飛行機を上昇・降下させるかのような感覚を植えつけられるが,現実の飛行機では,上昇・降下にはエンジン推力変化をもって行う.リアル試行のシミュレーションゲームや,市販シミュレータに付随するチュートリアルで着陸操作のレクチャを受けると必ず,飛行パスはエンジンパワーで,機速を機首上げ下げで制御するように指導される.詳しい解説は省略するが,これは機の力学的エネルギを考えると当然であり,2D/3Dの非線形質点運動モデルでも同じ挙動が現れる.
上述までに観てきた,ピッチ角,鉛直飛行パス角にエレベータ操舵とエンジン推力操作による運動が現れ,バンク角,横滑り角にラダー,エルロン操舵による運動が現れている.
非常に読み取り難いが,エレベータ操舵時には短周期の非常に減衰の大きな振動が観られるが,エンジン推力操作直後には短周期振動は全く観られない.飛行機は,迎角がどこか一定の値になるように自然とバランスが取られるように出来ているという事だ(意図的あるいは誤って”静安定”が”負”に設計されたものは除く).

3次元空間中の機の飛行軌跡全体も見ておこう.図中右側の,[x-east, x-north]= [0, 0]の位置がシミュレーション開始点で,機は図中左手へと移動してゆく.
尚,見易さのために3軸のスケールは合わせておらず,特に飛行高度(z軸)については大きく誇張された図である事は認識しておかれたい.

3次元軌跡で,軸スケールを変えた表示のものも記載しておく.x-east, x-north (x,y軸)はメモリ間隔を合わせ,飛行高度(z軸)については0 – 10,000 [m] に図示範囲を拡げておいた.

後書き・まとめ
毎度同様、ほぼ冒頭で述べたことの繰り返しとなるが、
- 飛行機の縦運動と横運動それぞれの状態空間線形時不変計算モデルと,機体フレーム・地上フレームの状態変数を繋げる微分方程式のモデルを組み合わせて,6自由度運動シミュレーションコンポーネントを作成した.
- 文献の付録に記載の,小型飛行機の空力微係数データを使ってシミュレーションを実施したところ,市販のフライトシミュレータで見られるものと似た挙動を確認できる.
モデル情報
- コンポーネントのフルパス: AircraftDynamics.RigidBodyFDM.Components.AirplaneLTISS_longiLatSprtd00
- 例モデルのフルパス: AircraftDynamics.RigidBodyFDM.Examples.sampleAircrafts.AirplaneLTISS_longiLatSprtd00_ex02
- githubのライブラリページリンク
- 例モデル実行用jupyter notebookファイル: RigidBodyFDM.Examples.sampleAircrafts.AirplaneLTISS_longiLatSprtd00_ex02_rev001.ipynb *動かすにはディレクトリ設定などの書き換えが必要なので、jupyterの基本的使い方を一通り知っている方向け。




コメント