先日、状態空間表現の紹介記事を出したが、背景に飛行機の運動モデル作成を進めていたというのがあった。仮定の置き方・リアリティの度合いによって幾つかモデルの種類が有るが、まず飛行力学の書で必ず取り扱われる縦横分離の線形時不変モデルから着手した。そして、今回、縦系運動・線形・時不変モデルのコンポーネントをリリースしたので本記事にて報告する。
記事を通して言いたいこと(結論)
例によって、冒頭で述べておく。
- Modelicaにて、飛行機の、縦系運動・線形・時不変シミュレーションモデルのコンポーネントを作成・リリースした。
- parameterとして無次元空力微係数を直接与える必要が有る。無次元空力微係数は既知として、運動予測や制御設計に用いることにフォーカスしたコンポーネントである。機体の飛行力学的形態を表すparameter、ex.翼アスペクト比や重心から尾翼空力中心までの距離etc、から空力微係数を算出する機能は別途コンポーネントを作成予定。
- 有次元空力微係数を直接与えての動作テストが、専門書の例題と完全一致。また、専門書付録データの無次元微係数を与えての動作テスト結果も定性的に妥当な動き。
モデル化対象(とその周辺について)
- 状態方程式中の状態変数は、線形化の基準となる飛行状態からの変化量であり、絶対値ではない。例えば、基準飛行状態のx-方向速度が100 m/s で、状態方程式中の第1状態変数の値が10 m/s となった場合、その瞬間のx-方向速度は110 m/s だ。
- 状態方程式中の入力信号は、線形化の基準となる飛行状態での入力値からの変化量である。例えば、基準飛行状態でエレベータ角が5 deg で、本モデル中のdeltaEの値が1 deg だったとすると、エレベータ角は6 degである。
- ”基準となる飛行状態”は、力・モーメントは釣り合い状態にあると仮定している。
- 基準飛行状態から大きく離れた運動の予測には使えない。(正確性が激減する。)
縦系運動
ピッチングと速度の運動と、ローリング・ヨーイング・横滑りの運動は互いに独立、影響を及ぼし合わないと仮定する。縦系運動モデルはそのうちの前者を取り扱う。
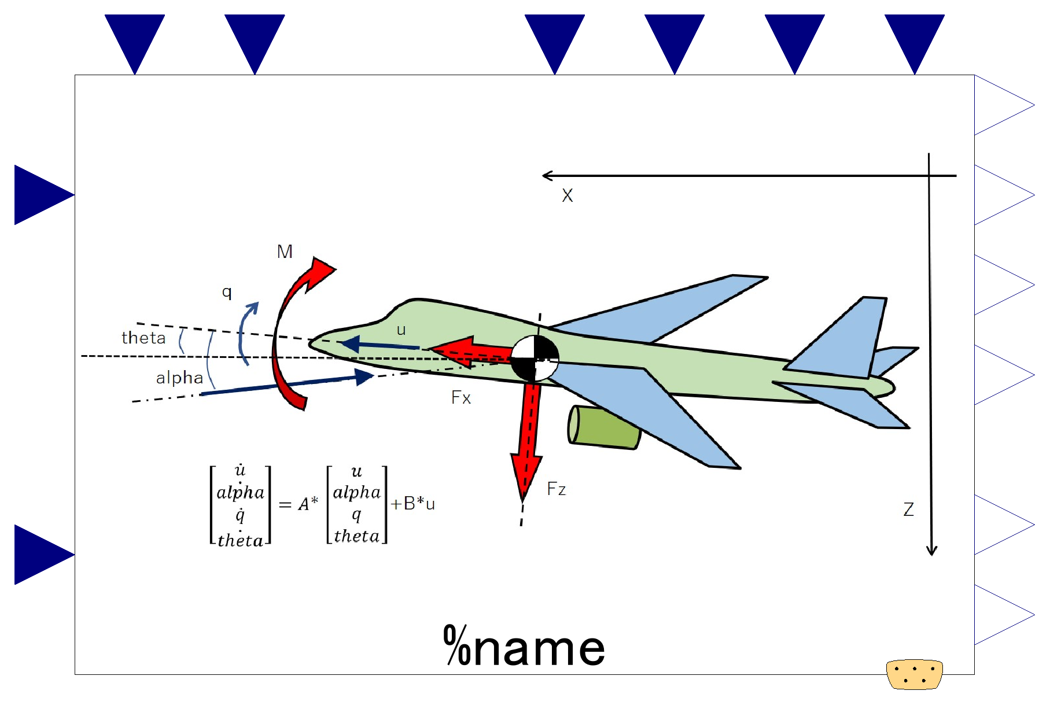
運動モデルを成す状態変数は、下図に記しているように、x(機体軸)方向速度、迎角、ピッチ角速度、ピッチ角の4つ。制御入力はエレベータ角操作とエンジン推力操作。微分方程式はx方向の力、z方向の力、ピッチングモーメントについて立式される。

線形・時不変 -微小攪乱-
本記事のコンポーネントが取り扱うのは、縦系運動の独立に加えて、”微小攪乱”と呼ばれる仮定を置いて線形化を施した飛行力学モデルだ。本記事では微小攪乱や線形化の過程は省略する。この辺を詳しく知りたい方は参考文献を載せておくので参照されたい。
詳細は省略するが、本コンポーネントを使う上で知っておかなければならない事は幾つか有り、下記に記す。
こんなものだろうか。総て線形化を理解していれば当然の事だとは思うが、本コンポーネントを利用されることがあれば、この辺りを認識して利用されたい。
一応、飛行力学の理論・式導出を詳しく載せている書籍を挙げておくので、興味の有る方はこれらを参照頂きたい。
参考資料:

|
Aircraft Dynamics: From Modeling to Simulation Amazon |

|
Flight Stability and Automatic Control Amazon |

|
Modeling and Simulation of Aerospace Vehicle Dynamics Amazon |

|
航空機の飛行力学と制御 Amazon |
コンポーネント
コンポーネントのインターフェイスや造りについて軽く触れておく。
下図の通り、本コンポーネントのインターフェイスは、real-inputとreal-outputのconnectorのみから成る。
real-inputのconnectorは大きく、入力信号、基準飛行状態、機体特性値、の3種類のグループに分かれている。このうち、基準飛行状態と機体特性値はparameterから与えるか、connectorを介して与えるかを選択できる。
real-outputのconnectorは、状態方程式の解と出力方程式の解の2グループ有る。状態方程式の解は、状態変数そのものではなく、paramterから与えた(もしくは複数のparameterから導出される)基準飛行状態の値に状態方程式の解を足した値が出力される。出力方程式の解は、x-方向とz-方向の加速度。線形化において、基準飛行状態は力・モーメントが釣り合っていると仮定しているので、こちらは出力方程式の解そのものを出力している。
なお、筆者の製作・公開しているコンポーネントは総てだが、connectorで出力されていない内部variableを取り出して別コンポーネントに繋げたい場合に備えて、汎用のexpandable connectorを1つ装備している。

コンポーネント内部の造りは下図の通り味気無く、大部分の処理・方程式はコードに記述されている。
ただ、規格化した方が都合が良い計算処理の塊はあり、それは別コンポーネントを創り、本コンポーネントに置いて呼び出している。内部コンポーネントで処理を行っているのは、与えた無次元空力微係数と飛行状態から有次元空力微係数を求める計算だ。この処理は今後LTVモデルや非線形モデルを作成するに当たっても登場する計算処理であり、部品として直ぐに使える状態にしておいた方が便利な事が判っている。
もう1つの、飛行機アイコンが描かれているコンポーネントは、シミュレーション共通の定数などを上層から呼び出すための”environmentAircraftDynSim”で、Fluidライブラリの”System”と同等のものだ。おまじないのようなものと見ておいて貰って差支え無い。

シミュレーションモデル
Diagram
動作確認用の例モデルを下図に示す。
この例では、入力信号、基準飛行状態、機体特性値の総てをreal-input connectorで与えている。飛行状態は機速と動圧だが、動圧は直接与えるには値が馴染みないものなので、飛行状態から流体状態を算出するコンポーネントを介す。飛行状態は飛行マッハ数と高度(と標準大気からのΔ気温)で指定するのが親しみ深い。
前項で述べた通り、一番左上の”environmentAircraftDynSim”は、Fluidライブラリの”System”同様におまじないよろしくシミュレーション実行の為に配置必須。
尚、機体特性値・無次元空力微係数は、(紹介済みだが)下記文献のAppendixに記載されているCessna 182(ベストセラーCessna172の兄弟みたいな機体)のものを与えている。

文献:

|
Aircraft Dynamics: From Modeling to Simulation Amazon |
シミュレーション実行
- エレベータ角(基準飛行状態からの変化)
- x-方向速度
- x-方向加速度(参考)
- 迎角(AoA)
- 迎角変化率(AoA加速度)(参考)
- ピッチ角
- ピッチ角速度
Input
Inputの値・動きが意図通りか、inpurtが反映されるvariablesを確認。
上げ舵と下げ舵を短いパルスをで与える。最初に短周期モードの鋭い振動が起き、その収束後に長周期モードの鈍い振動が長く続きながら元の飛行状態に向かって収束する動きを期待する。

Variables
速度には長周期モードの動きが強く発現する。なので余り複雑な挙動にはならず、概ね減衰を伴う単調な振動となる。
シミュレーション結果は、終始鈍い動きで次第に元の速度に向かって減衰・収束していっている。典型的な長周期モードの挙動で、速度変化も5 m/s 程度とフライトシミュレータ等で実際見られるような範囲。

_dt.png?raw=true)
迎角には短周期モードの動きが強く発現する。x-方向速度同様に、挙動は単調な振動に近い形となる。ただし減衰はx-方向速度よりも圧倒的に強いのが普通。
シミュレーション結果は、操舵直後に鋭く立ち上がり、瞬く間に減衰・収束し殆ど振動しない。こちらは典型的な短周期モードの挙動だ。フライトシミュレーションではAoAの動きを直接見たり体感することがほぼ無いため、この動きと値が妥当かの判断が難しい。ただ、C182は静安定性が高く迎角振動を殆ど起こさない機体の筈なので妥当だろう。

_dt.png?raw=true)
ピッチ角には短・長周期両方のモードが同じ位強く現れるので複雑な動きとなる。基本的には入力を与えた直後から短時間は短周期モードの動きが強く、徐々に長周期モードによる動きが支配的へと移ってゆく。
操舵に追随しようとピッチ角が急上昇しつつも、直ぐに舵角を戻したことで短周期モードの復元力によって折り返し急なピッチダウンに転じる。そして、すぐに逆操舵を加えたことでピッチ角が急降下し、またも復元力で折り返し逆方向に動く。その後は、直ぐに長周期モードが支配的になる。このとき長周期モードは機首下げ・増速の動きだったために、一度ピッチが上がりかけた矢先に直ぐにピッチダウンに転じ、操舵によるものよりも深いピッチダウンとなる。あとは、ゆっくりとピッチの上がり下がりを繰り返しながら元のピッチ角へと収束してゆく。
このあたりの動きはフライトシミュレータ(もしくは可能なら実機)で類似機を飛ばし慣れていれば馴染みのある挙動だ。短周期モード優位から長周期モード優位に遷るタイミングのような小刻みな動きは殆ど認識できないものの、操舵直後の復元力による折り返し挙動や、操舵を終えて放置した際の緩やかな振動などは実際に見て確認できるので、興味が有れば自身で確かめて見るのが一興だ。


フライトシミュレータを紹介しておく。中でもx-planeは挙動周りのリアリティが高い。そして、x-plane9は古いだけあって軽快で初代GPD pocketでも動くほどだ。x-plane10も今日の一般的ノートPCで動かすことはできる筈。なお、後継品ほどリアリティが増している筈だが、主な強化点はグラフィック周りと思われる。飛行力学モデルも全く同じではないのだろうが、バージョン間で飛行挙動が異なると感じたことは無い。

|
X-plane 9 Amazon |

|
X-plane 10 Amazon |

|
X-plane 11 Amazon |

|
Microsoft Flight Simulator X Amazon |

|
Microsoft Flight Simulator 2020 Amazon |

|
GPD Pocket Amazon |

|
GPD Pocket 2 Amazon |
後書き・まとめ
毎度同様、ほぼ冒頭で述べたことの繰り返しとなるが、
- Modelicaにて、飛行機の、縦系運動・線形・時不変シミュレーションモデルのコンポーネントを作成・リリースした。
- 有次元空力微係数を直接与えての動作テストが、専門書の例題と完全一致。また、専門書付録データの無次元微係数を与えての動作テスト結果も定性的に妥当な動きとなっている。
- 機体の飛行力学的形態を表すparameter、ex.翼アスペクト比や重心から尾翼空力中心までの距離etc、から空力微係数を算出するコンポーネントの作成。
- 横系のLTISS(線形時不変状態空間)モデル、縦・横分離仮定の下6自由度の機体運動全体をシミュレートするモデル、LTVSS(線形時可変状態空間)モデル、非線形モデルなどの作成。
- コンポーネントのフルパス: AircraftDynamics.RigidBodyFDM.Components.LongitudinalLTISS00
- 例モデルのフルパス: AircraftDynamics.RigidBodyFDM.Examples.sampleAircrafts.LongitudinalLTISS00_ex02
- githubのライブラリページリンク
- 例モデル実行用jupyter notebookファイル:LongitudinalLTISS00_ex02_rev001.ipynb *動かすにはディレクトリ設定などの書き換えが必要なので、jupyterの基本的使い方を一通り知っている方向け。
課題・今後の取り組み
モデル情報




コメント
[…] この記事に引き続き、飛行機の運動シミュレーション。今回は横系運動モデルのコンポーネント。線形・時不変なのは前回と同様。 […]