*記事微修正:2021/11/13
ターボチャージャーの回転慣性モーメント設定を、エンジン主軸の「1/100倍」と述べていたが、「1/10倍」の誤り。1/100の設定では、本記事で示すほどの応答遅れとはならず、2-3 [s] ほどで立ち上がり、静定する(それでも立ち上がりに1秒とかからないターボチャージャー未装備に比べて大きなラグには変わりないが。)。恐らく、1/100の設定の結果の方が、現実の車両用ターボチャージャーの挙動に近いと考えられるが、本記事ではターボラグの挙動を誇張したいので敢えて1/10の設定で話を進めている。
記事を通して言いたいこと(結論)
例によって、冒頭で述べておく。
- ターボチャージャーはピストンエンジンの出力を向上させる強力なデバイスだが、スロットルバルブ操作に対する時間応答に遅れを生じさせる事をシミュレーションで(定性的に、程度だが)確かめた。ターボチャージャの慣性モーメントをピストンエンジン本体のそれの1/10と仮定すると、非常に大きな応答遅れが生じた。
モデル化対象(とその周辺について)
ターボチャージャー(ターボ過給機)
自動車エンジンにおいて、効率向上と出力増強の両方でよく耳にする追加デバイス。
飛行機の世界でも活躍した。ピストンエンジンが飛行機用エンジンの主力だった第2次世界大戦当時には、大気密度の薄い高空でもエンジン出力を下げさせないためのデバイスとして、大きな役割を果たした。連合軍の爆撃機はターボチャージャーを搭載し、10,000 [m] の高空を悠々と飛行し、枢軸国側の戦闘機はターボチャージャーの実用化が上手くいかず、高高度性能が不足で迎撃に苦戦を強いられたりした。(実用化したとして物量の差は如何ともし難かった)

仕組みについても多少触れておこう。
下図の通り、ターボチャージャーは、タービンと、それに軸繋ぎの圧縮機から成る。バルブや熱交換機、バイパス流路など他にも付属物が有るが、ターボチャージャーの本質的な仕組みとは別なので今は無視する。
ピストンエンジンにおいて、燃焼ガスが膨張終了し、ピストンから出るとき、まだ圧力は外気の圧力よりも高く、排気経路の圧力損失を加味しても有り余っている。当然、温度・エンタルピも高い。通常のピストンエンジンは、この排気に残るエネルギ・圧力を排気口からただ外気に捨てている。これを有効活用しようということで登場するのがタービンだ。排気ガスをさらに膨張させ、有り余る圧力・エンタルピを回転機械仕事に変換して取り出す。
タービンが取り出した機械回転仕事の行先が、同軸上に繋がった圧縮機。圧縮機は吸気経路の途中に置かれ、吸気を圧縮する。これによりシリンダ流入空気の密度が上昇する。ピストンエンジンは機械回転数に対応して作動流体の体積流量が決まるので、同じ回転数における作動流体の質量流量が増え、熱サイクルが成す仕事が増大する。
このようにしてエンジンの出力を増強もすることから、サイズを小さくエンジンを強力にするデバイスとして扱われることもありつつ、動作原理として排気が持ち残しているポテンシャルを活用していることから、エンジンの効率(燃費)を向上させるデバイスとして扱われることもある訳だ。

wikipedia: ターボチャージャー
余談だが、現在車両用ターボチャージャーは米国企業2社、日本企業2社のほぼ寡占状態らしい。戦時中にターボチャージャーを造れない事で苦戦(+敗戦)した日本のメーカーが、寡占4社の2社というのは面白い話だ。
ターボラグ
ターボチャージャを装備すると生じる、過渡応答特性の変化であり、ターボチャージャーのデメリットの1つ。ターボチャージャーを装備しないピストンエンジン(以下、自然吸気エンジンと呼称。)に比べて、スロットルを操作し加減速する際の立ち上がりが遅く、静定までに時間が掛かる。
これは、主にターボチャージャーがエンジン本体(ピストン&シリンダ)の軸とは独立していることによる。圧縮機の回転はエンジンではなく、排気タービンの回転によって決定される。当然、タービンとピストン&シリンダは流路が繋がっているが、ピストン&シリンダからの排気流量とそれが持つ圧力・エンタルピが増加してもタービンの回転は急には上昇しない。風車に流速一定の風を当てると、回転数が増加して静定するまでタイムラグが生じるのと同じと考えれば良い。
それに加えて、”圧縮機が通せる流量”も回転数に依る(*回転に対して一義的には決まらない点には注意)ので、回転数が上昇するまでは圧縮機が吸気経路において、余計な絞りであるかのように流量増加の足枷となる。そして吸気流量が増えなければピストン&シリンダが生む出力が増大するのも遅れ、、と、更に出力・回転の上昇を遅らせてしまう流れとなる。
今回は、この過渡挙動を1Dモデルでシミュレーションしてみようと言う訳だ。
参考としてターボラグについて言及したwikipedia記事リンクを貼っておく。
Turbocharger lag*wikipediaにターボラグという日本語記事があるのだが、減速で生じる逆流云々に主に触れており、静定状態からただ加速した際には応答が遅れる事がないかのようにも取れるので、参考としてリンクを貼るのは避けた。この説明だと機械式スーパーチャージャーでも同じ問題が生じることになる。が、機械式スーパーチャージャーでは殆ど生じない問題の筈だ。(上記リンク記事にもスーパーチャージャーではこの問題は生じない旨の記述が有る。)
シミュレーションモデル
今回は、自然吸気かつ過渡応答(回転遅れ)を持つエンジンモデルと、それにターボチャージャーを追加したエンジン、2つのシミュレーションを実行し、時間応答を見比べる。
この記事のLyc〇ing 〇360エンジンの平均化モデルを基に両エンジンモデルを作成する。
- モデルのフルパス、自然吸気型〇360過渡モデル: PropulsionSystem.Examples.Engines.Transient.LycomO360_ex01
- モデルのフルパス、ターボチャージャー搭載〇360過渡モデル: PropulsionSystem.Examples.Engines.Transient.LycomO360turboCharged_ex01
- githubのライブラリページリンク
Diagram
自然吸気型の〇360:
過渡応答シミュレーション用に改修。回転慣性コンポーネントをエンジン軸に設けた。また、機械回転数拘束を解き、代わりに軸に回転抵抗(ダンパコンポーネント)を設けてエンジン出力に応じて回転数が増減するようにしている。調速機が搭載されていないプロペラを回すようなイメージだ。この時、ダンパの生む抵抗トルクは回転数に比例するので、回転数の立ち上がり≒エンジン出力の立ち上がりと観ることができる。
尚、回転慣性、回転抵抗の設定値は適当。何度かシミュレーションを実行して余り非現実的でない動きをするように与えている。

ターボチャージャ搭載〇360:
今回の本題はこちら。吸気経路上、スロットルバルブの手前に圧縮機を、排気経路上、排気合流の下流にタービンを配置。圧縮機とタービンは同軸で繋がり、間には回転慣性コンポーネントを繋ぐ。
ターボチャージャーのparameterも殆どは適当に値を与える。ただ回転慣性は、エンジン軸のものの1/10の値を設定する。実物の構造設計等に携わった事がないので知見不足なのだが、写真等を観ていると、遠心羽根車2つと軸だけから成るターボチャージャーの慣性モーメントは、クランクシャフトやピストン、フライホイール等が付いているエンジン本体の回転系よりは大幅に小さい筈だと思う。ここでは敢えて大き目と考えられる値を設定して、時間応答の遅れを誇張する。
*設計する側にとって、ターボラグをどこまで抑えられるかは、この慣性モーメントの値をどこまで小さく抑えられるかに大きく左右されることになる。

*両方の型で、クランクシャフトに機械回転数に比例する負荷を取り付けている(調速機の無いプロペラを回しているイメージ)。従って、エンジンのトルク-回転数カーブを取得するような、powerを固定して回転数を変化させるような操作でない事に注意されたい。
モデル情報
シミュレーション実行
基本的に、自然吸気型とターボチャージャー搭載型の両方を同グラフ上に重ね合わせて挙動を比較する。ただし、ターボチャージャー搭載型にしか無いvariableがあるので、それらの結果表示は当然ターボチャージャー搭載型のもののみだ。
- エンジン機械回転数:to_rpm_crankshaft.y
- エンジン軸出力:powerSensor1.power
- エンジン軸トルク:powerSensor1.flange_a.tau
- エンジン軸トルク vs. エンジン機械回転数:powerSensor1.flange_a.tau vs. to_rpm_crankshaft.y
- ターボチャージャー機械回転数:Cmp.Nmech
- ピストン&シリンダインテイクマニフォールド圧力
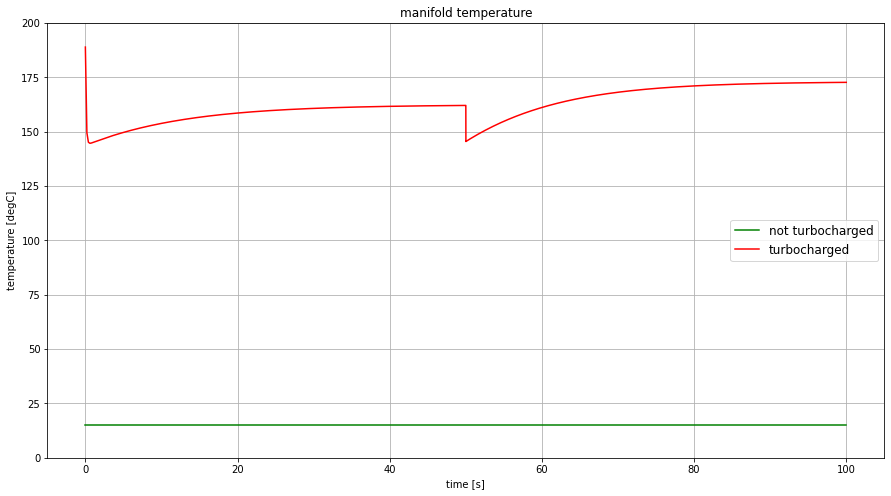
- ピストン&シリンダインテイクマニフォールド温度
- 加速開始直後の圧縮機圧力比低下挙動について
Input
Variables
*時刻0 [s] 直後から暫くの挙動は初期状態の与え方に起因するものであり、スロットル操作に対する挙動とは関係無いので無視して観て頂きたい。
圧倒的に違う。自然吸気型では数秒でスロットル操作に追随しているのに対して、ターボチャージャー搭載型は10-20 [s] も遅れが生じている。適当な設定とは言え、ターボチャージャーの慣性モーメントをエンジンの1/10も小さくしてこれ程の遅れというのは圧倒的な差だ。大型飛行機のエンジンならまだしも(機体の応答も遅いし、急加減速を要する場面も少ない。)、自動車のエンジンでこの応答遅れは非常に不快な操作性の悪さだろう。これを見ると、燃費の為だけでなく、ターボチャージャーを軽量化することがどれだけ重要かが理解できる。
*余談だが、高等プロペラ機は恒速プロペラを装備しておりプロペラ回転数は基本一定。なので、そういった装備を有する、プロペラまで含めたエンジンのトルク・推力応答を評価する場合は、調速機、プロペラ負荷などのモデルも用意する必要が有る。
*既出だが、当然、ターボチャージャーの慣性モーメントを更に小さくすれば、もっと応答が早い結果が得られることも確認している。エンジン主軸の1/100まで小さくすると2-3 [s]で立ち上がるようになる(それでも、自然吸気型よりは遅い)。

殆どエンジン機械回転数と同じ動き。

殆どエンジン軸出力と同じ動き。自然吸気型では一瞬少しだけオーバーシュートするのは、軸出力、機械回転数共に遅れが発生するが、機械回転数の方がレスポンスが遅いため(ターボチャージャー搭載型にも、オーバーシュートは無いが加速開始の瞬間に小さな段差のような動きは観られる)。

今回の計算内容的に参考情報でしかないのだが、自然吸気型とターボチャージャー搭載型で挙動が全く異なるのは読み取れる。ターボチャージャー搭載型の方が、その時間応答性の悪さが幸いして、トルクの急変は避けられている。また、静定に向かう動きが逆で、自然吸気型ではゆっくりと低下してゆくのに対して、ターボチャージャー搭載型はゆっくりと上昇している。これは前項のオーバーシュート有無という違いからも解る。
*自動車エンジンの性能曲線のような動き、機械回転が上がるにつれてトルクが下がるような動きなどといったものにはならない。エンジンクランクシャフトには比例定数一定の比例負荷が接続しており、出力・機械回転・トルクのいずれかを任意の値に固定するような操作は行っていない。

ターボチャージャー側の加速応答。加速開始から50 [s] 経過してもまだ立ち上がりきっていない。エンジン軸よりも更に遅れが大きい。

自然吸気型ではほぼ遅れ無しで上昇するのに対して、ターボチャージャー搭載型では機械回転のものに類似した遅れを伴う上昇となる。
興味深いのは、加速開始の瞬間、一度吸気圧が下がる点。これは吸気質量流量の変化と併せて特出しで後述する。

自然吸気型ではスロットルの操作に関係無く一定。ターボチャージャー搭載型では、インテイクマニフォールド圧力と類似した応答で遅れを伴って上昇する。空気は断熱で圧縮しても温度が上昇してしまうため、好ましくはないが上昇は避けられない。ターボチャージャー/機械式スーパーチャージャー搭載エンジンの多くで、吸気経路途中にクーラー(熱交換器)が装備されているのはこれに対処するため。
スロットルを開いた直後の、一瞬だが過給圧(給気マニフォールドの圧力)が急激に低下し、その後上昇する挙動に関する記述を複数の図と共にまとめて示す。
これも、ターボチャージャーの機械回転上昇の遅れによりもたらされたもの。コンプレッサーのPR-Wcマップ上の作動点の動きを考えてみれば判りやすい。スロットルを開いたことで、下流の流路抵抗が急減しガスが流れ易くなる。しかしながら、ターボチャージャーの機械回転数は殆ど増えていないので、作動点は同じ等回転線上に位置したままだ。同等回転カーブ上で通過質量流量を増すには、そのカーブの形から圧力比が低い所に作動点を移動しなければならない。このようにして、機械回転数が上昇するまでの間、過給圧は一時的に下がってしまうと言う訳だ。
同じことは、動翼の速度三角形のベクトルの動きを考えても解る。流路抵抗が激減し質量流量が増えるということは、入口側気流の軸方向速度成分が増す。この時、動翼機械回転数は変わっていない。すると、動翼と入口流が成す迎角は小さくなる。迎角が下がると翼が生じる揚力が減り、回転翼が流体に対して成す仕事が小さくなる。従って、圧力上昇が小さくなっていしまうと言う訳だ。
この辺り、システム全体と回転翼周りの流れを同時に意識して見ないと直観に反するような動きに見えるところだ。
*因みに、この挙動自体は回転慣性の大きさに依らず発生する。回転慣性を小さくして、ターボラグを小さくしても値の変化幅が変わるだけで、圧力比の瞬間的低下自体は起きる。
圧縮機圧力比:

吸気質量流量:

圧縮機作動点の軌跡 圧力比 vs. 入口修正流量:
*修正流量:軸方向マッハ数の近似なのだが、今回は質量流量と同義と見ておいて良い。作動流体の入口の温度・圧力が幅広くに変化する航空エンジンでは質量流量ではなく修正流量を観ることが重要となってくる。

—圧縮機マップから考える急加速時の挙動—

圧縮機回転翼の迎角に相当するvariable: Cmp.Rline
Rlineは、作動点が等回転線上のどこに位置するのかを示すvariableだ。軸方向マッハ数と周方向マッハ数の関係を定めるvariableでもあり、動翼と流入気流の成す角、迎角に相当するvariableとも言える。エンジン加速開始直後に作動線が下がり動翼の迎角が下がっていることは、このvarialbeの時間変化からも読み取れる。

参考文献:
後書き・まとめ
毎度同様、ほぼ冒頭で述べたことの繰り返しとなるが、
- ターボチャージャー搭載ピストンエンジンモデルを作成し、スロットルバルブ操作に対するエンジンの時間応答に遅れを生じさせる事をシミュレーションで(定性的に、程度だが)確かめた。ターボチャージャの慣性モーメントをピストンエンジン本体のそれの1/10と仮定すると、非常に大きな応答遅れが生じた。








コメント