*執筆途中だが公開ポリシーに則り公開。
2023.04.19
記事を通して言いたいこと(結論)
例によって、冒頭で述べておく。
- 流路網(FluidFlowNetwork)の代数方程式の計算を,非定常項を追加することで収束計算ではなく,微分方程式の時系列計算に置き換えてとして解いた(nodeが2つで,4未知数4方程式となるシステム).
- 本記事では,上記の立式過程も示す(流体は理想気体を想定).
- 代数方程式を収束計算手法で解くのに比べて,初期値が悪くても流量収支が釣り合うする解にたどり着く事ができ,過渡応答を評価したい場合だけでなく,計算収束性を改善したい場合にも利用できる手法である可能性が高い.
モデル化対象(とその周辺について)
- 独立変数
- Volume1, 圧力
- Volume1, 温度
- Volume2, 圧力
- Volume2, 温度
- 従属変数
- Volume1, 質量流量収支
- Volume1, 熱量流量収支
- Volume2, 質量流量収支
- Volume2, 熱量流量収支
流路抵抗3つ,ボリューム(Node)2つの直列流路
非定常項を加えて,状態方程式(微分方程式)を立式
式はボリューム1つに対してのみ示す.複雑な流路網ではボリュームの数だけ状態変数と状態方程式が増える.
Mass dynamics
Energy dynamics
状態方程式
定常状態を代数方程式として解く場合の独立・従属変数
シミュレーションモデル:
- モデルのフルパス: Scilab_misc/Examples_Xcos/FluidFlowNetwork/FluidFlowNetwork_DiffEqn_2vol_002.xcos
- githubのライブラリページリンク:Scilab_misc
- モデルのフルパス: Scilab_misc/Examples_Xcos/FluidFlowNetwork/FluidFlowNetwork_AlgebEqn_2node_003.xcos
- githubのライブラリページリンク:Scilab_misc
Scilab Xcosで作る:
Xcosなら関数を記述したブロックを繋げて複雑な計算式となるモデルを比較的容易に組立てられる.
一方で,XcosはModelicaとは異なり,自動で数式処理をおこなう機能は無い(Coselicaと呼ばれるModelica言語Blockは別).代数方程式/微分方程式で記述されるモデルを解けるようにするには,Inpuot/Outputが明示された処理block,積分器block,代数方程式ソルバblockを適切に繋げて処理を作る必要が有る.
その為,実は裏で”数式変形して方程式が宜しく解かれている”と言うことは起きない.代数ブロックの繋ぎ方がループになっていると(代数方程式をソルバで解く必要があるモデル),エラーが出て実行がなされない.これは,今回行いたい事には適している.
微分方程式(状態方程式)を立式して時間積分を行うモデル
Diagram
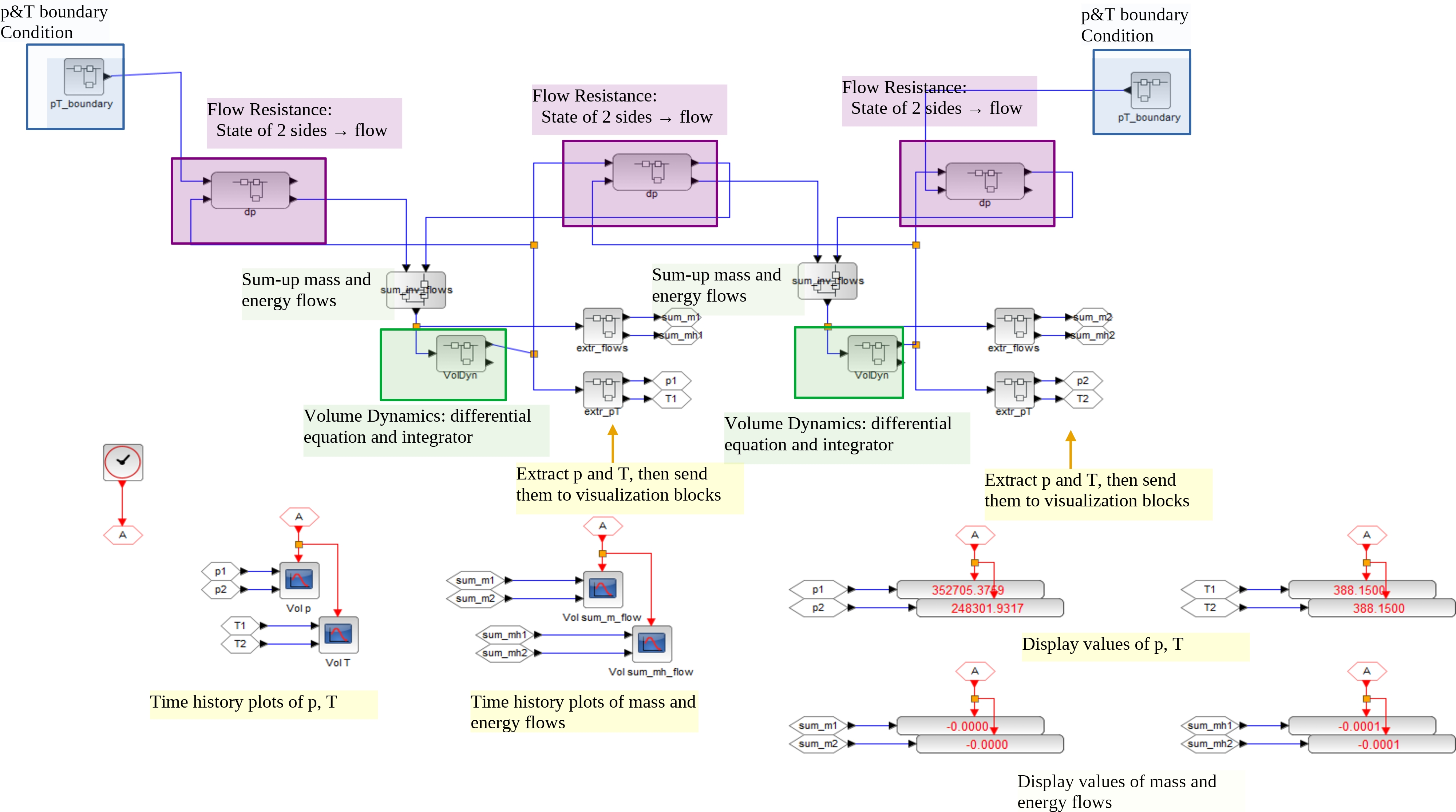
●シミュレーションモデル情報
VolumeDynamics blockの内部
代数方程式を立式してソルバBlockで解くモデル(検証用)
Diagram

●シミュレーションモデル情報
シミュレーション実行
Input
無し.固定の境界条件を与える.
Variables
以上





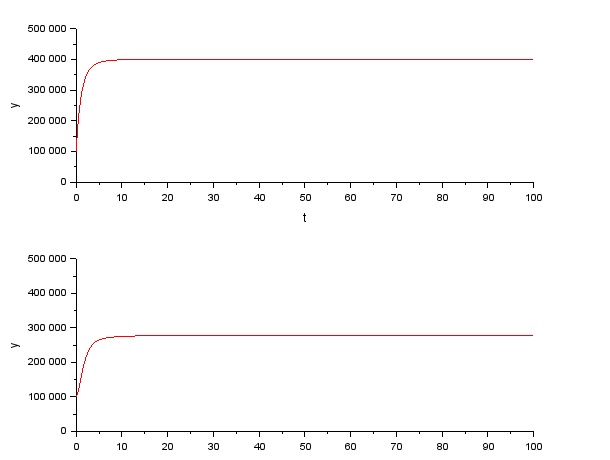

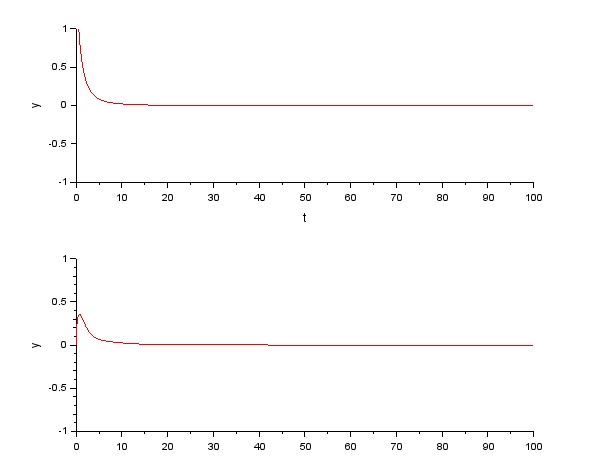








コメント