　今回はModelicaから離れて、主に制御工学分野で登場する「状態空間」と呼ばれる表現・概念について述べる。

　「状態空間」、「状態方程式」は制御工学分野のみで取り扱われる特殊な概念ではなく、汎用の微分方程式の表現方法の１つである（生まれや使われ所が主に制御分野なのだろうが）。便利な特徴が幾つか有り、状態空間の概要とそれら特徴を解説する。

　＊状微分方程式が解る程度に理工系一般知識を持ち、かつ状態空間て何だっけ？という、制御工学分野には疎い方向けの入門解説です。微分方程式て何？という段階の方には難易度が高すぎ、明日から状態空間表現を用いて実務をこなしたいという方には逆に薄すぎる内容となりますのでご了承あれ。

結論:状態空間とは何か

具体例や詳しい解説に触れる前にまずはこれを記そう。

Wikipedia（日本語）によると
Wikipedia（英語）によると
それでは何と言い表すか
線形システム
1. 時不変（LTI）システム
2. 時可変（LTV）システム
非線形システム
線形システム
1. 時不変システム：ばね・マス・ダンパー
2. 時可変システム：飛行機の微小攪乱線形化運動モデル –飛行力学–
非線形システム：

Wikipedia（日本語）によると

”制御工学において、物理的システムを入力と出力と状態変数を使った一階連立微分方程式で表した数学的モデル。”

“状態変数は、任意の時点でシステム全体の状態を表せるシステム変数群の最小の部分集合である。”

⇒…..解るようで何言ってるか解らない。日常で使う身には何のことか解るのだが、表現が抽象的かつ妙に小難しい。申し訳ないが、少なくともこれを読んで、”おぉ、状態空間表現使ってみよう”とはならないというのが筆者の印象だ。

Wikipedia（英語）によると

“In control engineering, a state-space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations or difference equations. State variables are variables whose values evolve over time in a way that depends on the values they have at any given time and on the externally imposed values of input variables.”

⇒日本語より解りやすい。しかし、やはり制御工学という極めて特定分野のみのものという印象を抱かせる記述という印象は残る。

それでは何と言い表すか

　制御工学に限定した言い方を取り除き、筆者自身の解釈を含めて述べると下記だ。

“オーダーが2以上の微分方程式（＊）を式に書き下すと、input/outputの関係性や変数同士の繋がりが解り難い。そこで、解りやすいように（また、変形など取り扱いもし易いように）、オーダーが１の微分方程式かつ微分項を左辺に寄せた式の集まりに書き下す。この表現を状態空間と呼ぶ。”　（＊各式が微分項を左辺に寄せた式であることは必須の条件ではない筈だが）

　＊世の中の微分方程式の殆どはオーダーが２以上だ。加えて、複数の微分方程式の変数同士が相互に作用しあうように繋がっていることも多い。なお、オーダーが１のみの微分方程式１つの場合、状態空間表現は一般的な微分方程式と何ら違いが無い。飽くまで、高オーダー・多変数のシステムを読みやすく表現するのに使われる道具だということを憶えておいてほしい。

システムの種類と書式

　下記に一般化した状態空間表現の書式を紹介するが、同時に、記述対象のシステムには幾つか種類が有るのでそれについて触れる。一般化した書式は、システムの種類によって多少異なるからだ。

　尚、切りが無いので、本記事では連続かつ時間領域のシステムに絞って話を進め、離散時間システム、ラプラス領域のシステム、Z領域のシステムに関しては触れない。

線形システム

　”線形な系”とは何かの解説を丁寧に行うと記事１つ分の尺は容易に埋まるので本記事では省く。改めて学びたい方は下記リンク先のwikipedia記事や、筆者が利用している動システム分野や自動制御の書に説明が有るので参照されたい。

恐らく、制御工学や動システム分野の書籍等で目にする殆どのシステムは線形のものだ。（＊後述するが、現実の物理システムの殆どは非線形で、制御や動特性解析に当たり、線形化したモデルを構築する。）

System Dynamics

⇒　項1.3, 項3.1

Automatic Control Systems

⇒　項2-3

線形性：Wikipedia

時不変（LTI）システム

　非線形の中でも制御工学、動システム分野で状態空間として登場するシステムの殆どはこの形。なので、本項の解説に重点を置く。

　”時不変”というのは、下記にリストアップする値の集まりのうち、状態変数・入力変数・出力変数以外の値（動特性を決定付ける変数、入力が状態変数に為す影響を示す値など）が時刻に因らず一定である事を意味する。言い方を変えると、微分方程式を書き下した時に、微分対象となる変数に掛る係数の値が変化しないという事。

　一般化した表現は下式のようになる。

x(t): 状態変数ベクトル。微分対象となる変数。変数は１つに限られず、複数の変数をベクトルの中に一纏めにして表す。これらの値は時間が進行するに従い刻々と変化する。　＊上に”・”が付いたものはxを一回微分したものである事を示す、一般的な数学表現。
A: 状態変数の項に掛る係数を集めて行列に格納したもの。安定性や固有周波数といった、動特性（のうち入力に因らず決まるもの）は本行列の値で決定される。
B: 入力変数の項に掛る係数を集めて行列に格納したもの。入力の状態変数へ与える影響を表す。飛行機の動挙動を例に挙げると、舵の効きの強さがこれに当たる。
u(t): システムへの入力（操作）をベクトルに格納したもの。
y(t): システムから取り出したい出力をベクトルに格納したもの。
C: 出力変数と状態変数を紐付ける係数を行列に格納したもの。
D: システムへの入力が出力変数に直接与える影響を表す係数を行列に格納したもの。

　上述した２つの方程式のうち、前者は状態方程式、後者は出力方程式と呼ばれる。出力方程式は”状態空間”自体の考え方とは直接関係無いのであまり意識する必要は無い。注目したい出力変数と状態変数の間、または入力変数と出力変数の間に代数方程式が挟まっている場合に必要となる方程式だ。

　一応、省略したものではなく、（具体例ではないが）行列の中身まで書き下したものの形を見ておこう。入力が２つ、微分方程式のオーダーが４、出力が３つのシステムの場合下記のようになる。式中のa, b, c, dの部分が、システムごとに値が異なる箇所だ。

　詳しい解説は、ここでは省略し具体例の項にて述べる。

時可変（LTV）システム

　前項と同様に線形ではあるが、係数行列A,B,C,Dの値が時間とともに変化するもの。

　一般化した表現もほぼ線形時不変システムのものと同じ。違いは行列A,B,C,Dに（ｔ）が付き、状態変数と同様に時刻により値が異なる事を示すようになっている点。省略せずに書き下した形も線形時不変システムと同じで、a, b, c, dの各値が刻々と変化するだけだ。

　因みに、現実のシステムには時可変なものは多数有るが、非線形システム同様に制御工学の例題にはあまり登場しない。

非線形システム

　前述の通り、世界の殆どはこれが該当する。時不変でも時可変でも、殆どの線形システムは何らかの仮定を置いて”線形化”処理を施したものだ。

　一般化した表現は下記の通り。

　システムごとに式の形から千差万別なため、一般化され得る箇所は限られている。共通しているのは、状態方程式がx, xの一階時間微分、u, tから（正確には、これらに加えてその他定数など）から成り立ち、出力方程式がx, y, u, tから成り立ついう点だけだ。

具体例

線形システム

時不変システム：ばね・マス・ダンパー

　動システム、制御工学、振動工学等で必ず登場する動システムの例だ。下記専門書の例をそのまま取り上げさせて頂く（どの教科書でも係数が異なるだけだが）。

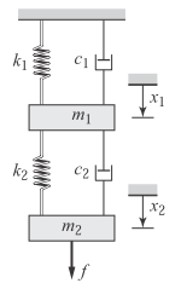
　一番基礎の例なので、状態方程式の一般型の形を導出するまで少し丁寧に述べるが、式変形の詳細は省く。

\begin{matrix} ２ つのmassの位置を変数に微分方程式を立てる 。 \\ 5 \ddot{x_{1}} + 12 \dot{x_{1}} + 5 x_{1} - 8 \ddot{x_{2}} - 4 \dot{x_{2}} = 0 \\ 3 \ddot{x_{2}} + 8 \dot{x_{2}} + 4 x_{2} - 8 \ddot{x_{1}} - 4 \dot{x_{1}} = f (t) \\ ここで 、 下式の通り ４ つの状態変数を定義する 。 記号xはすでに使っているのでここではzを使う 。 \\ z_{1} = x_{1} \\ z_{2} = \dot{x_{1}} \\ z_{3} = x_{2} \\ z_{4} = \dot{x_{2}} \\ これらを 2 つの微分方程式に代入し 、 左辺が状態変数の微分となる形に変形すると下記の ４ つの連立方程式が得られる 。 \\ \dot{z_{1}} = z_{2} \\ \dot{z_{2}} = - z_{1} - \frac{12}{5} z_{2} + \frac{4}{5} z_{3} + \frac{8}{5} z_{4} \\ \dot{z_{3}} = z_{4} \\ \dot{z_{4}} = \frac{4}{3} z_{1} + \frac{8}{3} z_{2} - \frac{4}{3} z_{3} - \frac{8}{3} z_{4} + \frac{1}{3} f (t) \\ 最後に 、 これらを線形連立方程式を行列表記に書き下すのと同じ要領で書き換えると 、 先に挙げた一般化された状態方程式を得る 。 \\ [\begin{matrix} \dot{z_{1}} \\ \dot{z_{2}} \\ \dot{z_{3}} \\ \dot{z_{4}} \end{matrix}] = [\begin{matrix} 0 & 1 & 0 & 0 \\ - 1 & \frac{- 12}{5} & \frac{4}{5} & \frac{8}{5} \\ 0 & 0 & 0 & 1 \\ \frac{4}{3} & \frac{8}{3} & \frac{- 4}{3} & \frac{- 8}{3} \end{matrix}] [\begin{matrix} z_{1} \\ z_{2} \\ z_{3} \\ z_{4} \end{matrix}] + [\begin{matrix} 0 \\ 0 \\ 0 \\ \frac{1}{3} \end{matrix}] f (t) \end{matrix}

出展：System Dynamics; William J. Palm III; Ex.5.1.1 (page 226)

System Dynamics

　以上のようにして、物理システムの図と微分方程式からLTI状態方程式の一般型が得られた。

　ここで、状態空間表現のメリットを見ておこう。具体例を見た後なので、多少実感しやすいのではないだろうか。

方程式の形が常に同じ。

　どのようなシステムであっても、（線形／線形化されたモデルで有る限り）方程式の形が常に一般型のもので変わらない。モデル化対象に応じて異なるのは各行列／ベクトルの次元（行、列の数）とその中に格納されている値が異なるだけだ。

関連する数学処理が常に同じ。

　前項から導かれる事柄だが、式の形が不変で値だけが異なるのだから、時間応答（微分方程式の解）を算出したり、動的特性を調べたりなど、種々の数学処理は対象システムが変わっても同じである。対象の物理システムがばね・マス・ダンパーだろうが、電気回路だろうが、同じ見方・考え方で特性を評価出来る。

コンピュータプログラムと相性が良い書式。

　総て行列表現で記されている故、上式の内容をコンピュータプログラムに落とし込もうとすると、”そのままコードに書き下せば良い”という場合が多い。特に、左辺=変数、右辺=式、というこの形だと、配列を使って行列演算を行うクラスなり関数なりが有れば式変形無しでそのままコードに落とし込める。

　また、前項からそのまま導かれることでも有るが、関連する前後処理に常に同じルーチン・関数を同じ勝手で使える事になる。＊これは状態空間表現に限らず、汎化度合いの高い数学表現総てに言える事である。

変数の変化に対する感度が一目瞭然。

　汎化された行列表現は単なる値の集まりではない。行列A, Bそれぞれの値は、状態変数-状態変数, 状態変数-入力の感度を示す。これは、微分方程式の集まりが総てオーダー１となっていることと、行列形式で整然と書き下されている事による。

　例えば、行列Aの[2,3]は、状態変数z2の、z3の変化に対する感度、と読み取る事が出来る。状態方程式に変形する前の、２つの微分方程式の形からは値を一瞥で読み取るのは困難だろう。これは動的挙動を調べつつ、設計変数（例えばダンパーの減衰係数）を調整する時などに役に立つ筈だ。

線形状態方程式を定義・立式すれば、数値的に線形化モデルがすぐ作れる。

— 係数行列を求める式の導出は必須ではない —

\begin{matrix} \frac{dx (t)}{dt} = f [x (t), r (t)] \\ Δ \dot{x} = A * Δx + B * Δu \\ [\begin{matrix} Δ \dot{x_{1}} \\ Δ \dot{x_{2}} \\ Δ \dot{x_{3}} \\ Δ \dot{x_{4}} \end{matrix}] = [\begin{matrix} \frac{\partial f_{1}}{\partial x_{1}} & \dots & \dots & \frac{\partial f_{1}}{\partial x_{4}} \\ ⋮ & ⋱ & ⋮ \\ ⋮ & ⋱ & ⋮ \\ \frac{\partial f_{4}}{\partial x_{1}} & \dots & \dots & \frac{\partial f_{4}}{\partial x_{4}} \end{matrix}] [\begin{matrix} Δ x_{1} \\ Δ x_{2} \\ Δ x_{3} \\ Δ x_{4} \end{matrix}] + [\begin{matrix} \frac{\partial f_{1}}{\partial u_{1}} & \frac{\partial f_{1}}{\partial u_{2}} \\ ⋮ & ⋮ \\ ⋮ & ⋮ \\ \frac{\partial f_{4}}{\partial u_{1}} & \frac{\partial f_{4}}{\partial u_{2}} \end{matrix}] [\begin{matrix} Δ u_{1} \\ Δ u_{2} \end{matrix}] \end{matrix}

出展：Automatic Control Systems, Golnarraghi and Kuo, 項4-9-2

Automatic Control Systems

　再度、前項から導かれる事柄。非線形モデルが手元に有って、制御や動特性解析のために線形化モデルが欲しい時、状態変数と入力を適切に定義し（普通は非線形モデルが有る時点で既知だが）、線形の状態空間方程式を書き下せば線形化は出来たも同然だ。次項の例に登場する式の行列Aの中身の様に、各値を求める式を導出しなくても、線形化モデルは得られる。行列A、Bは変数間の感度を示しているのだから、上式行列中に偏微分で示す各値を数値的に算出すれば良いだけだ。

　もう少し具体的に言うと、各状態変数と入力を１つずつ数値的に微小変化させ状態変数の応答を取れば、応答と微小変化の比が係数行列の値となる（例えばΔx1/Δx2がA(1,2)の値）。物理の方程式から線形化した式を導出するのは大変な作業であることが多いが、一度線形状態空間方程式を書けば半ば機械的に線形化モデルを導出できる。物理式を変形して導出するのと異なり、値に至る過程を物理的に追えなくて根拠を示せない、信頼度が低いという短所は有る。しかし、それについては評価したい条件・入力の範囲で非線形モデルと線形化モデルのシミュレーションを実施すれば済む。両社の時間応答解を比較すれば、非線形モデルが制御／動特性解析に十分使え得るものかを確認できる。

時可変システム：飛行機の微小攪乱線形化運動モデル –飛行力学–

　続いて、線形時可変システムの例を見ていこう。ただし、式導出や式自体についての踏み込んだ解説を省き、式自体の記載に関しても、1行目以外は省略する。本例題について詳しく学びたい方は、出展を載せておくので参照されたい。

\begin{matrix} [\begin{matrix} \dot{u} \\ \dot{α} \\ \dot{q} \\ \dot{θ} \end{matrix}] = [\begin{matrix} (\frac{\bar{q_{1}} S {- C_{D_{u}} - C_{D_{1}} + C_{{Tx}_{u}} + C_{{Tx}_{1}}}}{{mU}_{1}}) & \frac{- \bar{q_{1}} S (C_{D_{α}} - C_{L_{1}})}{m} & 0 & - g * \cos (θ_{1}) \\ ⋮ & ⋮ & ⋮ & ⋮ \\ ⋮ & ⋮ & ⋮ & ⋮ \\ ⋮ & ⋮ & ⋮ & ⋮ \end{matrix}] [\begin{matrix} u \\ α \\ q \\ θ \end{matrix}] + [\begin{matrix} \frac{\partial u}{\partial δe} & \frac{\partial u}{\partial δT} \\ ⋮ & ⋮ \\ ⋮ & ⋮ \\ ⋮ & ⋮ \end{matrix}] [\begin{matrix} δe \\ δT \end{matrix}] \\ 上式について 、 \\ \bar{q_{1}} = \frac{1}{2} ρ U_{1}^{2} \\ S : 主翼面積 \\ m : 機体質量 \\ U_{1} : 初期対機速度 （ 線形化の基準の定常状態での値を代表して使用 ） \\ ρ : 初期外気密度 （ 線形化の基準の定常状態での値を代表して使用 ） \\ θ_{1} : 初期ピッチ角度 （ 線形化の基準の定常状態での値を代表して使用 ） \end{matrix}

出展：AIRCRAFT DYNAMICS From Modeling to Simulation, Napolitano, 項8.4

Aircraft Dynamics: From Modeling to Simulation

　状態変数の数は４（前項の例と同様”オーダー４のシステム”），入力は昇降舵変化とエンジン推力変化の２つ。

　本例題にて注目して頂きたいのは、行列Aの中身（各値は”有次元空力微係数”と呼ばれる。）だ。各値の式は無次元微係数と呼ばれるもの（CDuなど）を有次元化している。無次元微係数は機体の設計変数で決まり（厳密にはそうでないものも有るが。）、飛行状態には依らない。だが、有次元化に用いられる変数には、機の飛行状態に応じて刻々と変化するものが有る。各々少し詳しく見ておこう。

主翼面積：ほぼ不変だろうが、フラップとよばれる機構の作動により大きく変化する場合が有る。

機体質量：短時間的に見ると変化しないが、機の質量のうち燃料が占める割合は大きく、巡行開始状態と着陸アプローチ開始時では値が全く異なる。

初期機体速度：飛行状態によって常に変化し続ける。

初期外気密度：飛行高度に応じて全く異なる値となる。

初期ピッチ角度：高運動を行う機でなければ、余り大きく変化する事は無く、最大-最小の範囲も小さいが、飛行フェイズに応じて変化はする。上昇時と降下時ではその差は誤差と呼ぶには大きい筈だ。

~~~線形化の仮定を満たしていても、常に扱いが同じとは限らない~~~

　時可変システムの、時不変システムと異なる重要な点は、線形化の基準とする状態に依って同じシステム（ここでは同じ飛行機）でも動的特性が全く異なり得るという事だ。制御則を策定したり、動特性評価を行う場合は、必ず線形化モデルを用意することと思うが、起こり得る総ての作動条件を網羅して設計・評価して置く必要が有る。飛行機の制御を例に挙げると、巡行開始条件で制御則を設計しても、同じもので着陸アプローチや低速飛行では意図通りの動作とはならない可能性が高い。飛行フェイズ毎に最適な制御測を設計しる必要が生じる。

非線形システム：

　非線形システムは、シミュレーションモデル製作時や”ダイナミックインバージョン法”などによる非線形システム制御設計をする際など正確さが最重要とされる場面で触れることになる。システムダイナミクスや制御一般では直接触れる機会は少ない。”非線形システムの状態方程式とはこういうもの”というのを紹介する程度に留め、極端に複雑な式を２つ挙げておく。

天体周りの宇宙船の質点運動モデル(2体問題) –軌道力学–

\begin{matrix} [\begin{matrix} \dot{X} \\ \dot{Y} \\ \dot{Z} \\ \dot{U} \\ \dot{V} \\ \dot{W} \end{matrix}] = [\begin{matrix} U \\ V \\ W \\ \frac{- μ}{{(X^{2} + Y^{2} + Z^{2})}^{\frac{3}{2}}} X + \frac{\sum F_{X}}{m} \\ \frac{- μ}{{(X^{2} + Y^{2} + Z^{2})}^{\frac{3}{2}}} Y + \frac{\sum F_{Y}}{m} \\ \frac{- μ}{{(X^{2} + Y^{2} + Z^{2})}^{\frac{3}{2}}} Z + \frac{\sum F_{Z}}{m} \end{matrix}] \end{matrix}

出展： Space Vehicle Dynamics and Control (AIAA Education Seriess), Wie; 項3.1

Space Vehicle Dynamics and Control (AIAA Education Series)

　軌道力学というと小難しいが、要は高校物理で登場する万有引力の式からなる運動方程式である。加速度が質点間の距離で決まり、式に累乗の形を含んでいたり、状態変数が分母に入っていたりする。また、質点が宇宙船の場合、エンジンを使うことで船体質量が変化するので時可変なシステムでもある。

飛行機運動モデル（6自由度） –飛行力学–

\begin{matrix} [\begin{matrix} \dot{u} \\ \dot{v} \\ \dot{w} \\ \dot{p} \\ \dot{q} \\ \dot{r} \\ \dot{X}' \\ \dot{Y}' \\ \dot{Z}' \\ \dot{Φ} \\ \dot{θ} \\ \dot{ψ} \end{matrix}] = [\begin{matrix} - qw + rv - g * cosθ + \frac{1}{m} T_{x} (δT) + \frac{{ρV}^{2} S}{2 m} C_{x} (δe, δT, u, α, q, θ, \dots) \\ ⋮ \\ ⋮ \\ \frac{(\frac{L}{I_{x}} + \frac{I_{xz}}{I_{x}} \frac{N}{I_{z}})}{(1 - \frac{I_{xz}^{2}}{I_{x} I_{z}})} \\ ⋮ \\ ⋮ \\ {cosψcosθ} * u + {- sinψcosΦ + cosψsinθsinΦ} * v + {sinψsinΦ + cosψsinθcosΦ} * w \\ ⋮ \\ ⋮ \\ p + {sinΦtanθ} * q + {cosΦtanθ} * r \\ ⋮ \\ ⋮ \end{matrix}] \end{matrix}

出展：航空機の飛行力学と制御, 片柳; 項1.4, 1.5, 1.6

航空機の飛行力学と制御

出展：AIRCRAFT DYNAMICS From Modeling to Simulation, Napolitano, 項1.10

Aircraft Dynamics: From Modeling to Simulation

　飛行機の運動モデルは状態変数が12個有り、どの方程式も複雑。状態変数同士の乗算や超越関数が多数登場する。飛行状態・フェイズに応じて値が変化する微係数も登場し、時可変でもある。精巧なフライトシミュレータを作るにはこれらを解き、且つ飛行状態・フェイズに応じた微係数を算出するルーチンなりデータテーブルなりが必要となる（＊blade element mehodやvortex lattice methodで機体のパーツ毎に働く力を算出し結果として機体全体に掛る力を算出する方式のものもある）。

　余談だが、Modelicaで記述するのは基本的に非線形システムの状態空間表現である。時間微分を含む式を記述する際は基本的的に1階微分で記述し（der(der(x))のように書けるのかも知れないが、式の見通しが悪くなるだけなので書くことはないだろう）、非線形の代数方程式の集まりは出力方程式に相当する。

　ただ、一般に目にする状態空間方程式と異なり、左辺がd/dt(状態変数)=, 出力変数= のような代入文の形になっておらず自由な形で記述されている（それがModelicaの特徴の１つ）。左辺がd/dt(状態変数)=, 出力変数=、という表現になっていないものを状態空間表現と呼んで良いかが怪しが。状態”空間”の名前は状態変数がベクトルに格納されていることに由来しているように解釈できるので。