”1自由度mass-spring-damper系”、に続いて機械系の例題。質点(Mass)、spring(ばね)、damper(減衰器)をそれぞれ1つ増やしている。”1自由度mass-spring-damper系”と並び、大学レベルの動システムや制御の講義の最初の方、あるいは数値計算プログラミングでルンゲ・クッタ法で解く方程式のお題で登場する定番の例題だろう。
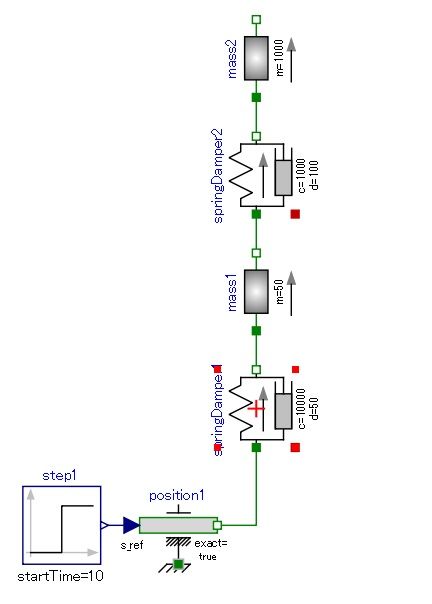
fig.1 quater car model diagram
このシステム、状態空間方程式に書き下すと4次元(4階の微分方程式)になるので、手計算で解析解を得るのは難しい。しかし、ステップ入力を与えると、mass2(車体を代表する質点)は減衰を伴うサイン波形、mass1(タイヤを代表する質点)は減衰を伴うサイン波が2つ重なった波形になるだろうと想像すると思う。matlabやルンゲ・クッタ法プログラム自作の例題によく使われるのはそのためだろう。
Modelicaモデルのダイアグラムはfig.1に示したもの。quater carの手書きの図と全く同じもので敢えて説明することは無い。
読者の方々が本計算を再現できるように、モデルコードのファイルをアップロードしてあるリポジトリへのリンクをページ最下に貼っておく。(GPL3ライセンス)
時間応答の計算結果は以下の通り。
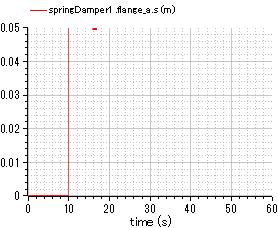
fig.2 displacement of road surface (input to system)
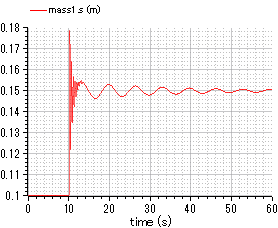
fig.3 position of mass 1
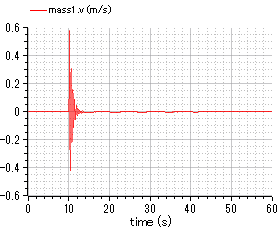
fig.4 velocity of mass 1
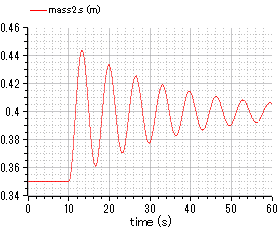
fig.5 position of mass 2
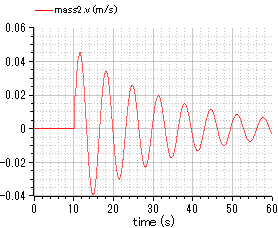
fig.6 velocity of mass 2
それらしい応答が出ている。こんな在り来たりな例題を解いても正直大して面白くない。演習紹介なので典型的な例題で、1自由度Mass-Sping-Damperの1ステップ上の1/4Carを選んだ。
前回と同様、注目して欲しいのはこの計算を回すのにかかる手間。OpenModelicaにある程度慣れた手だと、1自由度Mass-Sping-Damperのモデルスケッチから僅かな手間で本記事のモデルに作り替えられる。
MATLABのスクリプトでも常微分方程式は解けるし、非計算特化言語C++でも当然解ける。しかし、Mass-Spring-Damperの一式を1つ増やすだけで方程式の立て直しからプログラム書換までの手間は馬鹿にならないものになる。このように、システムの構成を変える必用が有る場合や、計算式がそれぞれは単純だが複雑に連立する場合に、オブジェクト指向かつ非因果(かつアイコンベース)の計算言語はとても強い。
先に述べたように今回取り上げた計算モデルをGithubリポジトリに上げているので、学習に役立てて頂ければ幸いだ。(ライブラリ、「SystemModels_xxxx」ごとダウンロードして読み込む方がトラブル無く、簡単かと思います)
フォルダ:SystemModels_20190120
ファイル名:quarterCar.mo



コメント