今回は、機体の運動を質点とみなして解くモデルを作成。 2自由度の運動方程式自体は飛行機に限定したものではなく、何にでも適用されるもので、複雑なものでない。運動方程式導出よりも、今回のコンポーネント作成でハードルとなったのは 後述する2点。
機体の運動を決める力は、速度ベクトルに沿う力・速度ベクトルに鉛直な力で、揚力・抗力・推力・重力ではない。姿勢・迎え角を介して変換が必要。
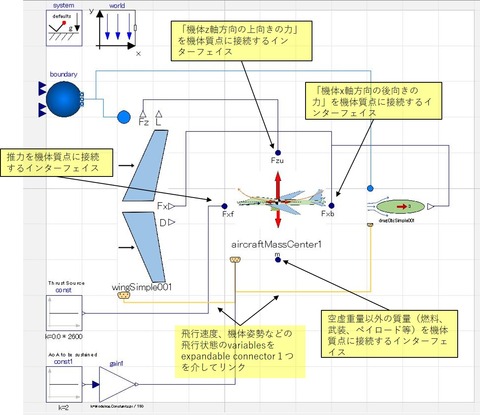
機体の構成設定に自由度を持たせられるように(エンジンの数を変える、エンジンの取り付け角を可変にする、翼をタンデムにする、抗力源として振舞う外部ペイロードを装備する、など)インターフェイスを備える。
- 1つ目は、質点に入力する力を、機体フレームに沿うもので統一し、運動方程式に必要な力への変換を質点コンポーネント内で完結させて、モデル組みの際にややこしい事を意識しなくて済むようにしている。
- 2つ目は、インターフェイスをmulti-portにすれば済む話なのだが、modelicaの配列の使い方に習熟が無かったため、作るときに多少苦労した。
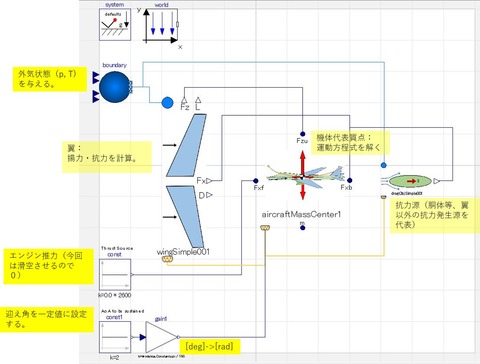
そして、作成した質点コンポーネントを使って作成した機体シミュレーションモデルが以下。
質点に、翼・抗力源(胴体抗力を代表)・エンジン・制御信号(迎え角指示値)・を繋いで「飛行機」を表現している。
parametersにはCessna172の判り得る情報から得た値と適当な値を入力。
エンジン推力は0を入力し滑空させる。Cessna172にそれなりに似たモデルが出来ていれば、滑空比(水平進行距離と高度低下の比)10から11くらいで滑空運動する筈。計算を回した結果が以下。
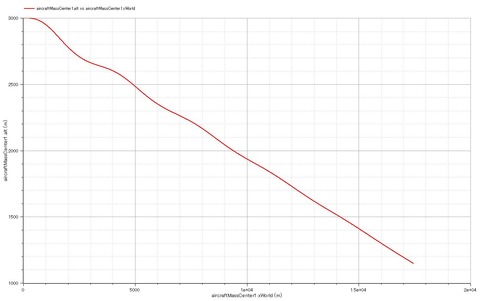
高度 vs.水平飛行距離
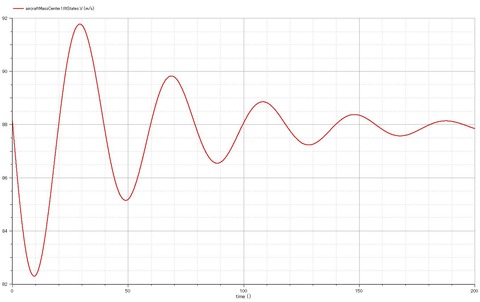
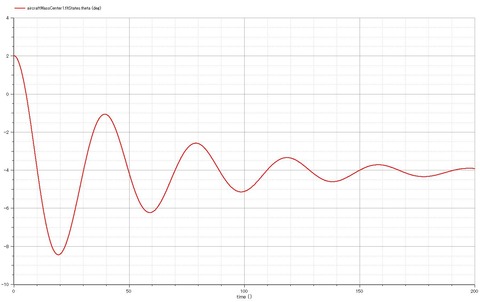
滑空比9くらい。10より少しより小さいが、適当な値を入れるざえを得なかったパラメータ故と思われる(抗力係数とか滑空比を決める重要なparameterが適当な値なのはいただけない。。。)。真っ直ぐな滑空ではなく波を伴ったような運動となっている。これは現実にも発生するもので、「フゴイド(phugoid)」と呼ばれる。位置エネルギーと運動エネルギーが交互に入れ替わる、減衰が小さく周期の長い振動。下図から読み取れるように、機体速度とピッチ角が減衰を伴うsin波を描き、位相が互いに逆転している。フライトシミュレータでも簡単に起きるので、興味をお持ちの方は試してみるといいかと。
ピッチ角 vs. 時刻
お次はフライトシミュレータ「X-Plane」でC172を滑空させたフライトレコード。
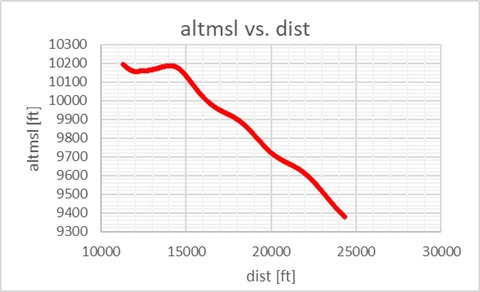
高度vs.水平飛行距離
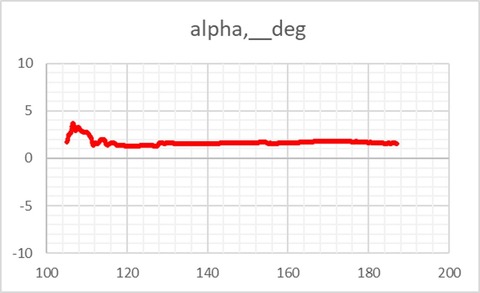
滑空比が11くらい。本物の模擬訓練機材に使われるソフトウェアだけあってデータとよく合っている。迎え角 vs. 時刻
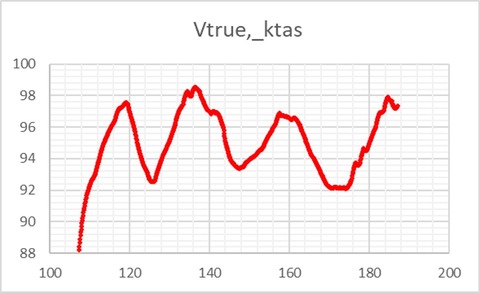
縦の舵は動かさないようにし、迎え角はほぼ一定となっている。(機体が縦運動についてプラスの静的安定性を持っているのであれば自然と一定値に収束する。)大気速度 vs. 時刻
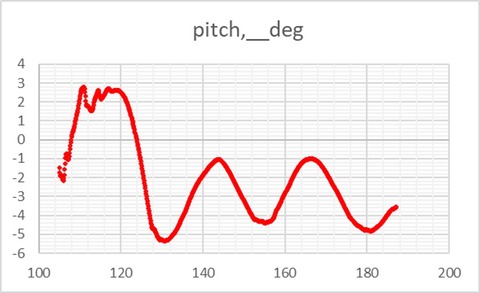
ピッチ角 vs. 時刻
綺麗なサインカーブにはなっていないが、近い形で減衰の弱い振動を繰り返している。ピッチ角と大気速度の位相がほぼ逆転しているのもModelicaのモデルの解析結果と同じ。これを観ると、今回作成したModelicaモデルは(パラメータの調整やDragのモデル化の甘さが残りつつも)それなりの再現度を有してると考えられる。次の目標は3次元質点運動、そしてその次は剛体運動解析モデルの構築だ。
今回はここまで。




コメント