かなり前だが、この記事にて、熱サイクルを通じて熱から仕事を得るには、”気体”相の流体を使う必要が有る(液相流体のみでは動力を発生させられない)ことを示そうとしたが行詰った。今回、やり方を変えてサイクルシミュレーションを再度試み、当時言おうとしていた事と逆の結果に辿り着いた。
記事を通して言いたいこと(結論)
例によって、冒頭で述べておく。
- 液相の流体だけを用いても熱サイクルを通じて仕事を取出す(動力を発生させる)事は出来る。最もシンプルな理想熱サイクルの計算で確認した。
- 液相流体でも可とは言っても、熱授受に応じて圧力・密度(体積)に変化が起きるという特性が必要条件。完全非圧縮性流体のパッケージを使うと計算自体回らない。
モデル化対象(とその周辺について)
ルノアールサイクル
熱力学を一通り履修していても聞いたことがない人がいるかもしれない。あまり実用的でないが故、実世界で殆ど利用される事が無い少しマニアックな熱サイクルだ。実はルノアール氏が世界初の内燃機関に用いた熱サイクルであり、熱力学発展史の中では非常に重要な存在だったりする。この機に心のノートにメモ位はしておこう。
実用的ではないと述べたが、その反面、熱サイクルとして最もシンプルという特徴もある。そのため、純粋に熱サイクルについて学ぶ題材として良いし、時折シンプルさが強く求められるところで実用に供されたりもする。この記事で登場した「パルスジェットエンジン」がその例で、第2次対戦時にドイツ軍のV1飛行爆弾の発動機に使われた。
下図の通り、加熱、膨張、排熱の3プロセスからなる熱サイクルだ。オットーサイクルやディーゼルサイクル等の一般的な理論サイクルと異なり、加熱前に圧縮プロセスが無い点が最大の特徴だ。この圧縮プロセスを省いていることにより、熱効率が低い。(それ故にオットーやらディーゼルやら別の熱サイクルに取って代わられた。)



古今東西エンジン図鑑―その生い立ち・背景・技術的考察

エンジン工学 ―内燃機関の基礎と応用
pulsejet wikipediaページ
Lenoir cycle wikipediaページ
シミュレーションモデル
- 実行モデルのフルパス: FluidSystemComponents.CommonAnyFluid.Examples.Thermodynamics.LenoirCycleIdeal00_ex03
- githubのライブラリページリンク
Diagram
ルノアールサイクル1巡の計算を行うコンポーネントを新造する。今回限りのモデルを造っても良いが、inputをインターフェイスで与えられるようじして汎用性を持ったblockにする。
下図の通り、サイクル計算に必要なインプットである、流体の最初の状態量、投入熱量、流体の質量/体積をconnectorを介して与えるようになっている。また、流体の最終状態量と生成仕事を取り出せるようにoutput real connectorを備えておいた(expandable connectorを置いてあるので不要かもしれないが)。
今回のモデリングは殆ど総てがコードの直書きなので、参考としてコンポーネントのソースを次項に記しておく。コンポーネントのコードも、実行用モデルのコードも総てgithubで公開しているのだが、アイコンの外観に関する箇所などが長大で見難いので、計算に必要な変数宣言と方程式記述箇所をハイライトして示す。

ソースコード
前述した通り、物理計算に必要な変数宣言と方程式部分をハイライトする。それ以外はインターフェイスだったり、アイコン外観だったりと使い勝手に関わる箇所なので無視して頂きたい。
FluidSystemComponents.CommonAnyFluid.Thermodynamics.LenoirCycleIdeal00
本サイクルは状態が3つのみなので方程式は少ない。
——————————————————————————-
within FluidSystemComponents.CommonAnyFluid.Thermodynamics;
block LenoirCycleIdeal00
/********************************************************
imports
********************************************************/
import Modelica.Constants;
import FluidSystemComponents.Types.Switches;
import FluidSystemComponents.Utilities;
/********************************************************
Declaration
********************************************************/
/* ---------------------------------------------
Package
--------------------------------------------- */
replaceable package Medium = Modelica.Media.Interfaces.PartialMedium annotation(
choicesAllMatching = true);
/* ---------------------------------------------
Switches
--------------------------------------------- */
parameter Switches.switch_input_ThermodynamicState switch_u_thermoState = Switches.switch_input_ThermodynamicState.use_T_for_ThermodynamicState "" annotation(
Dialog(group = "switch"),
choicesAllMatching = true,
Evaluate = true,
HideResult = true);
parameter Switches.switch_input_fluidQuantity switch_u_fluidQuantity = Switches.switch_input_fluidQuantity.use_mass "" annotation(
Dialog(group = "switch"),
choicesAllMatching = true,
Evaluate = true,
HideResult = true);
/* ---------------------------------------------
parameters
--------------------------------------------- */
//********** Others **********
parameter Integer nPts_hs_par[3] = {10, 10, 10} "" annotation(
Dialog(group = "Others"),
choicesAllMatching = true,
Evaluate = true,
HideResult = false);
parameter Integer nPts_Ts_par[3] = {10, 10, 10} "" annotation(
Dialog(group = "Others"),
choicesAllMatching = true,
Evaluate = true,
HideResult = false);
parameter Integer nPts_pv_par[3] = {10, 10, 10} "" annotation(
Dialog(group = "Others"),
choicesAllMatching = true,
Evaluate = true,
HideResult = false);
parameter Integer nPts_us_par[3] = {10, 10, 10} "" annotation(
Dialog(group = "Others"),
choicesAllMatching = true,
Evaluate = true,
HideResult = false);
parameter Integer nPts_pVol_par[3] = {10, 10, 10} "" annotation(
Dialog(group = "Others"),
choicesAllMatching = true,
Evaluate = true,
HideResult = false);
//********** Initialization Parameters **********
//--- fluidState_1 ---
parameter Modelica.SIunits.Pressure p_state1_init(displayUnit = "Pa") = 101.3 * 1000 "" annotation(
Dialog(tab = "Initialization", group = "fluidState_1"));
parameter Modelica.SIunits.Temperature T_state1_init(displayUnit = "K") = 288.15 "" annotation(
Dialog(tab = "Initialization", group = "fluidState_1"));
parameter Modelica.SIunits.SpecificEnthalpy h_state1_init(displayUnit = "J/kg") = T_state1_init * 1.004 * 1000 "" annotation(
Dialog(tab = "Initialization", group = "fluidState_1"));
parameter Modelica.SIunits.SpecificEntropy s_state_1_init = 7000.0 "" annotation(
Dialog(tab = "Initialization", group = "others"));
//--- fluidState_2 ---
parameter Modelica.SIunits.Pressure p_state2_init(displayUnit = "Pa") = 101.3 * 1000 "" annotation(
Dialog(tab = "Initialization", group = "fluidState_2"));
parameter Modelica.SIunits.Temperature T_state2_init(displayUnit = "K") = 288.15 "" annotation(
Dialog(tab = "Initialization", group = "fluidState_2"));
parameter Modelica.SIunits.SpecificEnthalpy h_state2_init(displayUnit = "J/kg") = T_state1_init * 1.004 * 1000 "" annotation(
Dialog(tab = "Initialization", group = "fluidState_2"));
parameter Modelica.SIunits.SpecificEntropy s_state_2_init = 7000.0 "" annotation(
Dialog(tab = "Initialization", group = "others"));
//--- fluidState_3 ---
parameter Modelica.SIunits.Pressure p_state3_init(displayUnit = "Pa") = 101.3 * 1000 "" annotation(
Dialog(tab = "Initialization", group = "fluidState_3"));
parameter Modelica.SIunits.Temperature T_state3_init(displayUnit = "K") = 288.15 "" annotation(
Dialog(tab = "Initialization", group = "fluidState_3"));
parameter Modelica.SIunits.SpecificEnthalpy h_state3_init(displayUnit = "J/kg") = T_state1_init * 1.004 * 1000 "" annotation(
Dialog(tab = "Initialization", group = "fluidState_3"));
parameter Modelica.SIunits.SpecificEntropy s_state_3_init = 8000.0 "" annotation(
Dialog(tab = "Initialization", group = "others"));
/* ---------------------------------------------
Internal variables
--------------------------------------------- */
Modelica.SIunits.SpecificEntropy s_state[3] "specific entropy, state 1" annotation(
Dialog(tab = "Variables", group = "start attribute", enable = false, showStartAttribute = true));
Modelica.SIunits.Mass massFluidCycle "mass of fluid in single cycle";
Modelica.SIunits.Volume Vol[3] "volume, state 1 - 3";
Modelica.SIunits.SpecificVolume v[3] "specific volume, state 1 - 3";
Modelica.SIunits.Heat Q_1_2 "heat injected into fluid, in process of const. vol. heat addition";
Modelica.SIunits.Heat Q_3_1 "heat rejected from fluid, in process of const. pressure heat addition";
Modelica.SIunits.Work WoutCycle "work output, single cycle";
Modelica.SIunits.Work W_2_3 "work, expansion, state 2 -> 3";
Real PR_2_1 "Pressure Ratio, P2/P1";
Real ER_3_2 "Expansion Ratio, Vol3/Vol2";
Real effThermal "Thermal efficiency";
//---
Modelica.SIunits.SpecificEnthalpy arr_h[4];
Modelica.SIunits.SpecificEnergy arr_u[4];
Modelica.SIunits.SpecificEntropy arr_s[4];
Modelica.SIunits.Pressure arr_p[4];
Modelica.SIunits.Volume arr_V[4];
Modelica.SIunits.SpecificVolume arr_v[4];
Modelica.SIunits.Temperature arr_T[4];
/* ---------------------------------------------
Internal objects
--------------------------------------------- */
Medium.BaseProperties fluidState[3](
p(start = {p_state1_init, p_state2_init, p_state3_init}, min = {0.0 + 1.0e-10,0.0 + 1.0e-10,0.0 + 1.0e-10}),
T(start = {T_state1_init, T_state2_init, T_state3_init}, min = {0.0 + 1.0e-10, 0.0 + 1.0e-10, 0.0 + 1.0e-10}),
h(start = {h_state1_init, h_state2_init, h_state3_init}, min = {0.0 + 1.0e-10, 0.0 + 1.0e-10, 0.0 + 1.0e-10}),
state(p(start= {p_state1_init, p_state2_init, p_state3_init})),
state(T(start= {T_state1_init, T_state2_init, T_state3_init}))
) "fluid states";
Utilities.arr_hs_const_p_00 curve_hs[3](redeclare package Medium = Medium, nPts_par = nPts_hs_par) annotation(
Placement(visible = true, transformation(origin = {-30, 70}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
Utilities.arr_Ts_const_p_00 curve_Ts[3](redeclare package Medium = Medium, nPts_par = nPts_Ts_par) annotation(
Placement(visible = true, transformation(origin = {-30, 40}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
Utilities.arr_us_const_p_00 curve_us[3](redeclare package Medium = Medium, nPts_par = nPts_us_par) annotation(
Placement(visible = true, transformation(origin = {-30, 10}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
Utilities.arr_pv_const_s_00 curve_pv[3](redeclare package Medium = Medium, nPts_par = nPts_pv_par) annotation(
Placement(visible = true, transformation(origin = {-30, -20}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
Utilities.arr_pVol_const_s_00 curve_pVol[3](redeclare package Medium = Medium, nPts_par = nPts_pVol_par) annotation(
Placement(visible = true, transformation(origin = {-30, -50}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
/* ---------------------------------------------
Interface
--------------------------------------------- */
PropulsionSystem.Types.SubelementBus subelementBus1 annotation(
Placement(visible = true, transformation(origin = {60, 100}, extent = {{-10, -10}, {10, 10}}, rotation = 0), iconTransformation(origin = {70, 100}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
Modelica.Blocks.Interfaces.RealInput u_p_fluidState_1(unit = "Pa", displayUnit = "Pa") annotation(
Placement(visible = true, transformation(origin = {-120, 20}, extent = {{-20, -20}, {20, 20}}, rotation = 0), iconTransformation(origin = {-110, 20}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
Modelica.Blocks.Interfaces.RealInput u_T_fluidState_1(unit = "K", displayUnit = "K") if switch_u_thermoState == Switches.switch_input_ThermodynamicState.use_T_for_ThermodynamicState annotation(
Placement(visible = true, transformation(origin = {-120, -10}, extent = {{-20, -20}, {20, 20}}, rotation = 0), iconTransformation(origin = {-110, -10}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
Modelica.Blocks.Interfaces.RealInput u_h_fluidState_1(unit = "J/kg", displayUnit = "J/kg") if switch_u_thermoState == Switches.switch_input_ThermodynamicState.use_h_for_ThermodynamicState annotation(
Placement(visible = true, transformation(origin = {-120, -40}, extent = {{-20, -20}, {20, 20}}, rotation = 0), iconTransformation(origin = {-110, -40}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
Modelica.Blocks.Interfaces.RealInput u_u_fluidState_1(unit = "J/kg", displayUnit = "J/kg") if switch_u_thermoState == Switches.switch_input_ThermodynamicState.use_u_for_ThermodynamicState annotation(
Placement(visible = true, transformation(origin = {-120, -70}, extent = {{-20, -20}, {20, 20}}, rotation = 0), iconTransformation(origin = {-110, -70}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
Modelica.Blocks.Interfaces.RealInput u_Xi_fluidState_1[Medium.nXi] annotation(
Placement(visible = true, transformation(origin = {-120, -100}, extent = {{-20, -20}, {20, 20}}, rotation = 0), iconTransformation(origin = {-110, -100}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
Modelica.Blocks.Interfaces.RealInput u_Qin(unit = "J", displayUnit = "J") annotation(
Placement(visible = true, transformation(origin = {-120, 80}, extent = {{-20, -20}, {20, 20}}, rotation = 0), iconTransformation(origin = {-110, 80}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
//-----
Modelica.Blocks.Interfaces.RealInput par_Vol1(unit = "m3", displayUnit = "m3") if switch_u_fluidQuantity == Switches.switch_input_fluidQuantity.use_Volume "valid if switch_u_fluidQuantity==use_volume" annotation(
Placement(visible = true, transformation(origin = {-60, 120}, extent = {{-20, -20}, {20, 20}}, rotation = -90), iconTransformation(origin = {-60, 110}, extent = {{-10, -10}, {10, 10}}, rotation = -90)));
Modelica.Blocks.Interfaces.RealInput par_massFluid(unit = "kg", displayUnit = "kg") if switch_u_fluidQuantity == Switches.switch_input_fluidQuantity.use_mass "valid if switch_u_fluidQuantity==use_mass" annotation(
Placement(visible = true, transformation(origin = {-20, 120}, extent = {{-20, -20}, {20, 20}}, rotation = -90), iconTransformation(origin = {-20, 110}, extent = {{-10, -10}, {10, 10}}, rotation = -90)));
//-----
Modelica.Blocks.Interfaces.RealOutput y_WoutCycle(unit = "J", displayUnit = "J") annotation(
Placement(visible = true, transformation(origin = {110, 80}, extent = {{-10, -10}, {10, 10}}, rotation = 0), iconTransformation(origin = {110, 80}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
Modelica.Blocks.Interfaces.RealOutput y_p_fluidState_3(unit = "Pa", displayUnit = "Pa") annotation(
Placement(visible = true, transformation(origin = {110, 20}, extent = {{-10, -10}, {10, 10}}, rotation = 0), iconTransformation(origin = {110, 20}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
Modelica.Blocks.Interfaces.RealOutput y_T_fluidState_3(unit = "K", displayUnit = "K") annotation(
Placement(visible = true, transformation(origin = {110, -10}, extent = {{-10, -10}, {10, 10}}, rotation = 0), iconTransformation(origin = {110, -10}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
Modelica.Blocks.Interfaces.RealOutput y_Xi_fluidState_3[Medium.nXi] annotation(
Placement(visible = true, transformation(origin = {110, -100}, extent = {{-10, -10}, {10, 10}}, rotation = 0), iconTransformation(origin = {110, -100}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
Modelica.Blocks.Interfaces.RealOutput y_h_fluidState_3(unit = "J/kg", displayUnit = "J/kg") annotation(
Placement(visible = true, transformation(origin = {110, -40}, extent = {{-10, -10}, {10, 10}}, rotation = 0), iconTransformation(origin = {110, -40}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
Modelica.Blocks.Interfaces.RealOutput y_u_fluidState_3(unit = "J/kg", displayUnit = "J/kg") annotation(
Placement(visible = true, transformation(origin = {110, -70}, extent = {{-10, -10}, {10, 10}}, rotation = 0), iconTransformation(origin = {110, -70}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
//********************************************************************************
equation
/* ---------------------------------------------
Connections, interface - internal variables
--------------------------------------------- */
connect(curve_pVol[3].u_m, massFluidCycle);
connect(curve_pVol[3].u_Xi, fluidState[3].Xi);
connect(curve_pVol[3].u_s, s_state[3]);
connect(curve_pVol[3].u_pLower, fluidState[1].p);
connect(curve_pVol[3].u_pUpper, fluidState[3].p);
connect(curve_pVol[2].u_m, massFluidCycle);
connect(curve_pVol[2].u_Xi, fluidState[2].Xi);
connect(curve_pVol[2].u_s, s_state[2]);
connect(curve_pVol[2].u_pLower, fluidState[1].p);
connect(curve_pVol[2].u_pUpper, fluidState[2].p);
connect(curve_pVol[1].u_m, massFluidCycle);
connect(curve_pVol[1].u_Xi, fluidState[1].Xi);
connect(curve_pVol[1].u_s, s_state[1]);
connect(curve_pVol[1].u_pLower, fluidState[1].p);
connect(curve_pVol[1].u_pUpper, fluidState[2].p);
//---
connect(curve_hs[3].u_Xi, fluidState[3].Xi);
connect(curve_hs[3].u_p, fluidState[3].p);
connect(curve_hs[3].u_sUpper, s_state[2]);
connect(curve_hs[3].u_sLower, s_state[1]);
connect(curve_hs[2].u_Xi, fluidState[2].Xi);
connect(curve_hs[2].u_p, fluidState[2].p);
connect(curve_hs[2].u_sUpper, s_state[2]);
connect(curve_hs[2].u_sLower, s_state[1]);
connect(curve_hs[1].u_Xi, fluidState[1].Xi);
connect(curve_hs[1].u_p, fluidState[1].p);
connect(curve_hs[1].u_sUpper, s_state[3]);
connect(curve_hs[1].u_sLower, s_state[1]);
//---
connect(curve_pv[1].u_pUpper, fluidState[2].p);
connect(curve_pv[1].u_pLower, fluidState[1].p);
connect(curve_pv[1].u_s, s_state[1]);
connect(curve_pv[1].u_Xi, fluidState[1].Xi);
connect(curve_pv[2].u_pUpper, fluidState[2].p);
connect(curve_pv[2].u_pLower, fluidState[1].p);
connect(curve_pv[2].u_s, s_state[2]);
connect(curve_pv[2].u_Xi, fluidState[2].Xi);
connect(curve_pv[3].u_pUpper, fluidState[3].p);
connect(curve_pv[3].u_pLower, fluidState[1].p);
connect(curve_pv[3].u_s, s_state[3]);
connect(curve_pv[3].u_Xi, fluidState[3].Xi);
//---
connect(curve_Ts[3].u_Xi, fluidState[3].Xi);
connect(curve_Ts[3].u_p, fluidState[3].p);
connect(curve_Ts[3].u_sUpper, s_state[3]);
connect(curve_Ts[3].u_sLower, s_state[2]);
connect(curve_Ts[2].u_Xi, fluidState[2].Xi);
connect(curve_Ts[2].u_p, fluidState[2].p);
connect(curve_Ts[2].u_sUpper, s_state[3]);
connect(curve_Ts[2].u_sLower, s_state[2]);
connect(curve_Ts[1].u_Xi, fluidState[1].Xi);
connect(curve_Ts[1].u_p, fluidState[1].p);
connect(curve_Ts[1].u_sUpper, s_state[3]);
connect(curve_Ts[1].u_sLower, s_state[1]);
//---
connect(curve_us[3].u_Xi, fluidState[3].Xi);
connect(curve_us[3].u_p, fluidState[3].p);
connect(curve_us[3].u_sUpper, s_state[3]);
connect(curve_us[3].u_sLower, s_state[2]);
connect(curve_us[2].u_Xi, fluidState[2].Xi);
connect(curve_us[2].u_p, fluidState[2].p);
connect(curve_us[2].u_sUpper, s_state[3]);
connect(curve_us[2].u_sLower, s_state[2]);
connect(curve_us[1].u_Xi, fluidState[1].Xi);
connect(curve_us[1].u_p, fluidState[1].p);
connect(curve_us[1].u_sUpper, s_state[3]);
connect(curve_us[1].u_sLower, s_state[1]);
//--- u ---
fluidState[1].p = u_p_fluidState_1;
fluidState[1].Xi = u_Xi_fluidState_1[1:Medium.nXi];
if switch_u_thermoState == Switches.switch_input_ThermodynamicState.use_T_for_ThermodynamicState then
fluidState[1].T = u_T_fluidState_1;
elseif switch_u_thermoState == Switches.switch_input_ThermodynamicState.use_h_for_ThermodynamicState then
fluidState[1].h = u_h_fluidState_1;
elseif switch_u_thermoState == Switches.switch_input_ThermodynamicState.use_u_for_ThermodynamicState then
fluidState[1].u = u_u_fluidState_1;
end if;
Q_1_2 = u_Qin;
//--- par ---
if switch_u_fluidQuantity == Switches.switch_input_fluidQuantity.use_Volume then
Vol[1] = par_Vol1;
elseif switch_u_fluidQuantity == Switches.switch_input_fluidQuantity.use_mass then
massFluidCycle = par_massFluid;
end if;
//--- y ---
y_p_fluidState_3 = fluidState[3].p;
y_T_fluidState_3 = fluidState[3].T;
y_h_fluidState_3 = fluidState[3].h;
y_u_fluidState_3 = fluidState[3].u;
y_Xi_fluidState_3[1:Medium.nXi] = fluidState[3].Xi;
y_WoutCycle = WoutCycle;
/* ---------------------------------------------
Eqns describing physics
--------------------------------------------- */
massFluidCycle = Vol[1] * fluidState[1].d;
v[1] = 1.0 / fluidState[1].d;
s_state[1] = Medium.specificEntropy(fluidState[1].state);
//--- state1 - state2 ---
// const. vol. heat addition, closed system
Vol[2] = Vol[1];
fluidState[2].d = massFluidCycle / Vol[2];
v[2] = 1.0 / fluidState[2].d;
fluidState[2].Xi = fluidState[1].Xi;
Q_1_2 = massFluidCycle * (fluidState[2].u - fluidState[1].u);
s_state[2] = Medium.specificEntropy(fluidState[2].state);
PR_2_1 = fluidState[2].p / fluidState[1].p;
//--- state2 - state3 ---
// isentropic expansion, pressrue of after-expansion fixed, open system
fluidState[3].d = massFluidCycle / Vol[3];
v[3] = 1.0 / fluidState[3].d;
s_state[3] = Medium.specificEntropy(fluidState[3].state);
fluidState[3].Xi = fluidState[2].Xi;
s_state[3] = s_state[2];
W_2_3 = massFluidCycle * (fluidState[3].h - fluidState[2].h);
Vol[3] / Vol[2] = ER_3_2;
//--- state3 - state1 ---
// const. pressrue heat rejection, open system
fluidState[1].p = fluidState[3].p;
Q_3_1 = massFluidCycle * (fluidState[1].h - fluidState[3].h);
//---
WoutCycle = (-1.0) * W_2_3;
//---
if 0.0 <= u_Qin then
effThermal = WoutCycle / Q_1_2;
else
effThermal = 0.0;
end if;
//----------
for i in 1:3 loop
arr_p[i]= fluidState[i].p;
arr_h[i]= fluidState[i].h;
arr_u[i]= fluidState[i].u;
arr_T[i]= fluidState[i].T;
arr_s[i]= s_state[i];
arr_V[i]= Vol[i];
arr_v[i]= v[i];
end for;
arr_p[4]= fluidState[1].p;
arr_h[4]= fluidState[1].h;
arr_u[4]= fluidState[1].u;
arr_T[4]= fluidState[1].T;
arr_s[4]= s_state[1];
arr_V[4]= Vol[1];
arr_v[4]= v[1];
annotation(
defaultComponentName = "LenoirCycle",
Icon(graphics = {Rectangle(fillColor = {255, 255, 255}, fillPattern = FillPattern.Solid, extent = {{-100, 100}, {100, -100}}), Text(origin = {0, -80}, extent = {{-100, 10}, {100, -10}}, textString = "%name"), Bitmap(origin = {2, 10}, extent = {{-94, 78}, {86, -70}}, imageSource = "/9j/4AAQSkZJRgABAQEAlgCWAAD/2wBDAAMCAgMCAgMDAwMEAwMEBQgFBQQEBQoHBwYIDAoMDAsKCwsNDhIQDQ4RDgsLEBYQERMUFRUVDA8XGBYUGBIUFRT/2wBDAQMEBAUEBQkFBQkUDQsNFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBT/wAARCAMLA5kDASIAAhEBAxEB/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/8QAHwEAAwEBAQEBAQEBAQAAAAAAAAECAwQFBgcICQoL/8QAtREAAgECBAQDBAcFBAQAAQJ3AAECAxEEBSExBhJBUQdhcRMiMoEIFEKRobHBCSMzUvAVYnLRChYkNOEl8RcYGRomJygpKjU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6goOEhYaHiImKkpOUlZaXmJmaoqOkpaanqKmqsrO0tba3uLm6wsPExcbHyMnK0tPU1dbX2Nna4uPk5ebn6Onq8vP09fb3+Pn6/9oADAMBAAIRAxEAPwD9U6KKKACiiigAooooAKKKarrIMqwYZIyDnkHBH50AOooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDx79rH9oTTf2Y/gf4g8bXhjlv4Y/s2lWchx9qvXBEUf0BBdv9lGNfBn/AASb/bP1HXPGWvfCzx3rD3t3rl1ca1ot7dP8zXcjNLdQZ/2yTKo4+YSdSwFdt8QtPuf2+P29F8EXEErfCX4QzF9XR1IS9vs4MbA8HdIhjGescUpH3q+XPgj+zdqXxO/ZZ8e+PPAyyWvxO+HXjmbVtKurNB588McNu7xL/tIUEqDn5kKgfOTQB+4NFeQfsmfHyH9pb4C+GPHi232K9vImg1C1CkLFdxMUmCZ6oWXcvJ+VgDyCB6/QAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFOx0ew02e7ns7K3tZryTzrmSCJUaeTAG9yB8zYAGTzgCvgv8A4JDZh8H/ABltz1i8ZzZ7H/Vgf0r9AK+AP+CS/wC7tfjxD18vxnL83rww/pQB99W1rDZwrDbwxwRLkiONQqjJyeB7k1LRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUV8GftpeANX+KH7bXwA8M6Rr+oeF/t+laul7qmlP5d1FaBQZ1jfHyM6AxhhyN+e1Yv7SvwD0D9gvQdD+NPwYl1Twx/ZOr2sPiTRW1O5u7XWrOaQI/nLM7/OCwwcgDcSAGANFP3lCUtFJ2+fM4p+l+u++ml2SupSjHVpX/AAvb18vTXU/Q2iorW4S8top4zmOVA6n2IyKlpvTRiTUldBXwB/wSp/c+Iv2jbY/ei8Zvnsfvzjp/wGvv+vgD/glz+7+JH7UMPXy/GbfN6/vrsf0pDPv+iiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigD4J/bV8ReLfCv7cX7O2p+CdDXxNr1vp+ruujNOsBvIRHmeNHb5VcxB9pPG4LU/xi1Xx7+3snh74b6d8KPGPw48BR6rb3/inXPHNiunyNDC24W9rFvYylj/GOAQuQBzXuHxQ+AHiHxt+1p8HfihY3mmRaB4OtNSgv7a4lkF1K1xA0aGJRGVIBYZ3OvHTNe/06fu06d9bNu3Z87a+Wzt/mwqa1Jcul4pX+Vn8+l/8AgDY41hjVEG1FAUD0Ap1FFISVlZBXwB/wTN/c/HX9re2P3ovGfPY/8fWoDp/wGvv+vgD/AIJu/u/2nP2y4evl+M1+b1/03VB/SgZ9/wBFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFfAH/BPP8Ac/te/tkR9d3ilHz/ANvmonH6/pX3/XwB+wX+5/ba/a8j67tdjfP/AG9XZx+v6UAff9FFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXlPgX9prwH8RvjN4w+F+h39xP4r8KxCXUIZbcxx/f2OI2PL7GKBjjH7xcE84xP2yv2krH9lz4F614ukaKTW5R9h0WzkI/f3jg7OO6oA0jeyEdSK/E39mn4veKPgD+1HpvxH8SLqfl6frx07xZczK7MPtJlW4Sb+9JhJ5Ap6tBn+HIAP6I6KitrmK8t4ri3lSeCVBJHLGwZXUjIYEcEEd6loAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAK+AP2If3P7fH7WMfXdqEb5/7bynH6/pX3/XwB+xz+6/4KK/tTR9dzxPn/ALag4/WgD7/ooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA+JPip+zr46/aU/bq0e/8b6Q1r8E/ANrDd6WksqPDrF4ypI37sHP+swr7hjbbgfx5r5R0T4Px/Giz/wCChmlLAJtT0zxONc04hNzrcWt7q0uEH954xJF/21NfsTX5/wD/AATjUN+1N+2iCMg+M1BB/wCv7VaAO7/4JT/E3xL8Sf2TNLXxGFlXQL2TRNOvPMVmmtIUjMYcD7pQN5Yz1VFPvX2LX58f8E3Vm+Cnx8/aC+AV1IUtdH1Qa5pFuc/8e7kIz888xPY/rX6D0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFfAH7J/wC5/wCCmX7TcfXdbQvn/gUJx+v6V9/18Afsz/uf+CqH7R8fXdpMD5/8Azj9f0oA+/6KKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACvgD/AIJw/wDJ037aH/Y5r/6XarX3/XwB/wAE4f8Ak6b9tD/sc1/9LtVoAqftFW7/AAE/4KdfBf4jRv8AZ9H8f2x8OaiF+USzgC3Bc+g86ybn/nl19P0Kr4i/4K5eB7nW/wBmG18X6aXg1XwXrlpqkV1D/rI43byG2+mHkhbPbZX1f8IfH0HxU+FfhDxjbbRFr2k2uo7Vx8jSxK7IcE4KklSMnBBFAHXUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV8Afs/fuf+Ctv7QkfXd4ct3z/AMA004/X9K+/6+APgr+5/wCCxfx5j67vB9s+f+2WjnH6/pQB9/0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFfAH/AATh/wCTpv20P+xzX/0u1Wvv+vgD/gnD/wAnTftof9jmv/pdqtAH2F8evh2nxb+CnjnwayK8mtaPdWcO7+GZo28pv+Avtb8K+a/+CSfxGk8a/skWWiXbsb/wnql1o7rMxMnllhcR5BOQAJzGOn+qx2r7Rr88P2Jf+LKft+ftG/CRx5Fjqzr4j06NjhFTzBKqIM8ny75enaHnpQB+h9FFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFfAHws/c/8ABZL4xZ583wZBjH/XHSuv5Gvv+vgDwP8Auf8Agsl8Qu/m+DIvw/c2P/xP60Aff9FFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXwB/wTh/5Om/bQ/7HNf8A0u1Wvv8Ar4A/4Jw/8nTftof9jmv/AKXarQB9/wBfnv8AtUKvwV/4KVfs/wDxIDta6b4rgfw5elSQkkmWgBfHYC8tzzx+6B7V+hFfEX/BXLwVc6t+zLY+MdO/dap4L16z1RLhRlkjdjAcf9tJIW/4BQB9u0Vzfw18aW/xI+HXhfxZaALa67pdrqcaj+FZolkA/Ddj8K6SgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACvgDw/8A6P8A8FkvE2P+W/gxM446Q2/X1+6K+/6/P+DMP/BZK4yM+b4MGPb9yv8AhQB+gFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXwB/wTh/5Om/bQ/7HNf8A0u1Wvv8Ar4A/4Jw/8nTftof9jmv/AKXarQB9/wBeeftEfD0fFj4E+PvCAh8+fWNEura3XGcXBiYwsBkciQIfwr0OigD48/4JR/EY+PP2O9BsJnZ7zwxfXWiTFjzhXE0fHoI541/4BX2HX55f8E+s/B79r79pP4NTMYoBfjX9LtiMBLfzTyOMZMV1ad/4eB1x+htABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFfAGo/wCj/wDBZLS8f8t/BjZxx/yxk/P7or7/AK+APFX7n/gsl4Ozz5vgyTGP+uN31/I0Aff9FFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXwB/wAE4f8Ak6b9tD/sc1/9LtVr7/r4A/4Jw/8AJ037aH/Y5r/6XarQB9/0UUUAfn38cEPwR/4KpfCLxmiLBpPxC0ttAvG6Ga5AMKjPsWsPXpj0r9BK+Fv+CuXhW7T4H+EviPpMajWPAniS1v0uCP8AVRSEIfzmW1/KvtHwb4os/HHhDQ/EentusNYsYNQt2znMcsayIfyYUAbFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV8AfET9z/wWS+F3fzfBk34fudR/wDif1r7/r4A+Ln7n/gsl8Es8+b4MuMY/wCuOr9fyNAH3/RRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV8Af8E4f+Tpv20P8Asc1/9LtVr7/r4A/4Jw/8nTftof8AY5r/AOl2q0Aff9FFFAHln7U3w3/4W7+zn8RfCSQfaLrUdFuBaRgZzcovmQcf9dUjryP/AIJe/EgfEb9jXwckkvnXvh959Cuf9nyX3RL+EEkFfV9fnr/wT4uB8G/2r/2jPgbKq21rDqR8Q6RbgEbbcuB9OYbiz4/2T1HQA/QqiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAK+APjp+6/4K/fAGQ/dbwrcIMdc+Xqv+Ir7/r4A/aM/df8ABWD9naQ/dbQp0GOudt//AIigD7/ooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAK+AP+CcP/J037aH/AGOa/wDpdqtff9fAH/BOH/k6b9tD/sc1/wDS7VaAPv8AooooAK/Pr9pRV+Bf/BTL4HfEZAtrpPje0fw3qLA4Es4JgDOT0A+0WZ7D9z9a/QWvij/grX8OLjxX+y5/wlemu0Gr+CdWttXinhJEqxs3kPtI6YMscmeMeVmgD7Xorjvg38QIfit8JfB3jK3K7Nd0m11AqpHyPJErOn1ViVPuDXY0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXwB+1F/o//BUL9muYfefTpozjg4zcjr/wI19/18Aftdfu/wDgpN+y/IfutHMgx1zvk/xFAH3/AEUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFfAH/BOH/k6b9tD/sc1/8AS7Va+/6+AP8AgnD/AMnTftof9jmv/pdqtAH3/RRRQAVyvxW8A2vxU+GPivwbev5Vtr2l3OmvLt3GLzYmQOB6qWDD3ArqqKAPh7/gkr8QbvVPgHrnw61lmj8Q/D/W7jTJ7WQ5eKGR2kQE+0ouUA7CMfQfcNfnp4Td/wBmv/gq54g0V2eDwx8XtKN9AuQsQvgGk3Me7eZDcqB1zdL61+hdABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV8Aftn/uP+ChX7Ks3TdcSx/L1/wBco/L5v519/wBfAH7dH7r9uv8AZJkP3W1WRBjrn7Rb/wCIoA+/6KKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACvgD/gnD/ydN+2h/wBjmv8A6XarX3/XwB/wTh/5Om/bQ/7HNf8A0u1WgD7/AKKKKACiiigD4P8A+CsfgvUNL+HvgL4z+Ho1HiL4c6/b3YmKEqsMkiFS2OoE8duMejt+P2l4D8Zaf8RfA/h/xVpLM2l65p9vqVqXGG8qaNZFyOxwwyPWsr4z/DWz+MXwm8XeCb7aINd0yexEjjiKR0Ijk+qPtYe6ivlf/gk78SLzXPgBq3w71v8AdeI/h3rE+k3FuxJkSB3eSMsT6SfaIwB0EIoA+26KKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACvgD9v79x+2f+x9N03eIXjyvX/j6sh+Xzfzr7/r4A/wCCi37r9rD9jKQ/dbxeyDHXP23TP8RQB9/0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFfAH/BOH/k6b9tD/ALHNf/S7Va+/6+AP+CcP/J037aH/AGOa/wDpdqtAH3/RRRQAUUUUAFfnlpuP2Yf+Crd9ZkraeFfjBpf2hBhvLW/5PJ/56NPDJ6gfax0zx+htfDv/AAVh+Ht9dfBnwz8VdADx+J/htrUGp29xGpYxwySRq5wD/DKls+ewRugJNAH3FRXJfCP4jaf8Xvhf4V8a6WQLLXtNgv0j3BjEXQFo2IJG5G3KR2KkV1tABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXwB/wAFKP3X7Rn7Hlx08rxmeR1/4/NNPH5V9/18Af8ABTr918Yv2Ubjp5XjPqOv/HxYnj8qAPv+iiigAooooAKKKKACiiigAooooAKKKKACiiqGva/pvhXRb3WNZv7fS9KsYmnur27lEcUMajLMzHgADuaTaSuxpNuyL9FfKh/4KLeCdXeS48HfD34pfEXQI3KN4i8K+EpbjT8g4b53ZG47/L2r2L4I/tFeAP2iNDudS8Da/Hqn2NxFe2UkbQXdm/PyzQuA6chgDjB2nBOKpJtXRLaW56TRRRSGFFFFABRRRQAUUUUAFFFFABXwB/wTh/5Om/bQ/wCxzX/0u1Wvv+vgD/gnD/ydN+2h/wBjmv8A6XarQB9/0UUUAFFFFABWD488F6b8RvBOveFdZjMula1YzafdKuN3lyoUYjIOCA2QexANb1FAHwd/wSj8ZajoPg34gfA7xIxTxJ8OddngEZY7TbyyPnZnqomSZsjjEqHvk/eNfnZ8esfsn/8ABST4e/FCJFtPCPxMtv7A1uXIVEuN0cbO56KoP2OUknJ8uU1+idABRRRQAUUUUAFFFFABRRRQAUV4LfftpfD3T/2mIPgfKmq/8JVLsj/tBbeP+zkneEzJbtL5m4SFBwNmMkDOa96oWsVJbMHpJxe4UUV5F4J/ac8LePPDPxN1zT7DV4bT4f6jfaZqiXMMSyTS2ke+UwASEMpH3SxQk9QKlyUU2+iu/RW1/FFRi5NJLd2+b/4Y9dorivgv8WNI+Onwv8P+O9Btr200jWoGnt4dRREuFUOyYdUd1Byp6Me1drWkouLcZbozjJTipR2YUV5n8efj94e/Z58P6Dq/iOz1O9ttZ1q20K3XS4o5HWecOUZw8iAINhyQSemAa9MqVqrr0/J/qino7P1+Wq/RhRRRQAUVwvxb+NXhb4JaVo994pu5rddY1S30awit4Gle4upmwiDHC8BiWYgAKec4Bzvip8fvD3wi8afDzwxrFnqdzf8AjjUm0rTpLGKN4opQFJaYtIpVfnHKhj14oWrSXV2+emn4r7weibfRX+Svr+D+49LooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACvgD/gqZ+68c/szXHTyvGa8jr/rbU8flX3/AF8Af8FXv3Wofs93HTy/GcfI69Yjx+VAH3/RRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXxH/wUMupPiF8SvgB8FLieSHw7408Qm51uON2T7TbWxjbySR2bex68FVPavtyvk79vf4U+K9atPh38VvAWlya74t+GmsDVRo8GfNv7Jiv2iKMD7z4jXgckbsAnAM3jGpTlP4VKLfpf8k9X5Ir3nCcYfE4yS9bP/hl5n1LpGkWPh/S7TTNMs4dP06ziWC3tbaMRxQxqMKiqOAAAAAK+JP2kNNj+BP7eHwM+IPhmL7BJ4+upvDPiSC3wqXynylikde7gyA7uv7lPx7bxJ/wUG8A698FbnxV8O/Ffg+XxbCI5D4V8aa1Fo118rgzwFZWBEoXeqsMpuwckdfnz4c/HzSP+Chn7YXws1WCGHwn4c+HdnJqx0vVr2H7Zf6lLj5LdA2ZY42jjO8Doh3Bd6itaacsTBvo9f8ADZ39U1detjOXLGhNdGml6/Z9GpWfomfppRRRUFBRRRQAUUUUAFFFFABRRRQAV8Af8E4f+Tpv20P+xzX/ANLtVr7/AK+AP+CcP/J037aH/Y5r/wCl2q0Aff8ARRRQAUUUUAFFFFAHzH/wUZ+BjfHb9lfxPZ2UDT6/oAGv6WIwS5lgVjIigckvC0qgf3ivpXS/sQ/HZf2h/wBmnwf4qnuRc63Hb/2brGW3OL2ABJGb0Mg2S49JRXuzKGUgjIPBBr86/wBktpP2Sf26viT8A7km28IeMN3iPwrEMrFGcM4jQHr+6WSItnk2ajvwAforRRRQAUUUUAFFFFABWD488Z6d8OvBOveKdXl8nS9GsZr+5f0jjQu2PfAwB6mt6vjH/gpV4nv/ABN4Y8B/Azw9O0ev/E3W4bKZoxkw6fE6vPIfYMYyfVVes6nNJKFP4pNJer0/Df0RpDlT5p/CtX6LVnzrD8E/Eni/9hfxJ8e3V4fijfeKW+J1nNj54YYJCEjHcoIfMkUehUV+hHgn4+6B4q/Z1sPi7I/k6FJoJ1u6VCGMISIvNH15ZWV1x6rXhtp/wThtrHQYdEt/2gvjdb6NDbCzj06HxYEtkgC7REsYh2hAvy7cYxxXiv7N/hTV9C8IftJ/sdXt60mrafZX1x4Wmu2ANxZ3URC9gANzwucdDM/pV1JJQq06Wml4r/ClFr/wFRf/AG6yILmlTnU72k9vid/wk2v+3j1L4T6t+1J+0b4NtPizpHxB8OfDzSNS33Wh+BJ/DyX0F3bBiIvtd2zCaMyY5aPsQwAztHK/sO+MfEFn8CP2ofFM9oPD3iqHxXruovagrMLK8W1Vyg3DDhHGORg46V2X7JH7Yvwt8G/s0eHtA8deLdN8D+K/BNgNG1nw/rkwtr6OW2Gw+XA3zy7lUECMMcnHUYrgv2Q/Fy+Pv2cf2tPEsdpNYRax4i8QX8dtcIUkjWSyDqrKejAEZHrSxNqccQqT91U5Wf8A29Gzv57/AC0sa4e83S9qtXON18pXVvLb563PVPAf7RXxOm/YF8KfEfTtAuviZ8T9WtRHFbW1j8ss73EkYmljt1ULGirk7QudoGRnNc58WNE/ay+D/wAM9Z+Jr/G3w/4huNEsm1W/8Ft4RghsfLRd80Ud0G85wqhsE7S2OozXlX/C5fGPwW/4Je/BfUPCGoN4e/tS8h0vU/EqWv2htHs5LiffOqYIzlVXOP4sDDFSOe/aK8N/APTPgh4llPx78YfHnxje6dMNH0Wbxm+rBLry2YTG2tiPLjjAMjeb8oCEHPQ6Yr3Kldw0tJpfg7Jbdeu+2yOfCe/SoKevNFN/ldv5dNt3uei/t6/FO6+J37F/wP8AiBpuk79Q1fxRomqw6Ujk7p2t538kNjJ+f5QcV2/xLuP2sfgv4DvvizfeP/DHi2LS4f7R1f4cw+H0t7S3tVG6Zbe9DGaRkXJy/XBOGwFPivxs106B/wAE4f2WtXgtZdTew8QeH7lbS1G+Sdo4Z28tAOrErtA9a99/aW/bZ+EfiH9mfxNbeE/F+neLPEXi3SZtH0jw5pUom1KW4uozEiPbLmSIgvkh1HTHJIBVa9P23slqpuy3+zGyt1vt+VjSjap7D2uzgrv/ALeld36W3/O53HxR/aG8Z658DvAPib4K+E5PEut+OprOOzmvLaWWz0eGZQXubvy+Qsedp5Azk8hcHx349at+09+yb4Bn+Kd/8YtG+KGhaVcQHVvDF34Ut9NQQyyrGTDNCxkJDOoG4jg5OcbTyvxg1/xz+y/+z1+zR8L5fFNx8NtH1gx6Z4r8ZWqCSXS/kRzAkhBEZJkk/edhFkHAavHP20vDfwM0X4F6vb+H/jD4q+O3j+XyprF77xdJrqabEsqGe4kEBEUahCV/eAnMgx6iazVOU5U9lNpddFbS3bzfdu9kmKgvaRpxqdYpvpvfW/fTZeWl3Y9t/wCCmGmeLPGWl/BDxLonjk6P4c1TxLpENnoraRDMba/l8149QMzHc+1GVfII2HGSea9V+MXxE+J/wT8afsyeDrjx7/wkN34i8QSab4k1X+x7W1/tWIFCP3QVhBgPj92wPGc1wH7dF9b6f+zj+zfrFxPHDpVl4s8O3VzeM37qGIW7EuzdAuOc1u/tc+KNG8afHD9kPWfD+r2Ou6PdeMJmt9Q025S4t5gPKUlJEJVsEEcHqDW3KoVfZx29sl8vc0+d36rTZK2HM6lFVZb+xb+dp6/Kyfk9d279R8UfjR8UPit+0ZqnwT+Dmq6Z4OXw7p0V/wCJvGmo2Iv5LR5gGigt7diI2cqVJ38HLfd2fNr/AAj8QfHn4b/HCD4efEucfE/wlqmnyXmn/EHS9D+wfZZ0yWt7yOLMUe4A7cHJO3k5IXzTSfGukfst/wDBQD4pXXxDvovDnhn4m6fp97oviHUD5NiZrWLy5beSZvlR+WPzEDG3ONy59R0T9rR/it+0/ovw/wDhXJovjHwVYadNf+LfE1qXuIbNiMW0ME8b+Uzsw5GG4Jx9xsZ0dY02tXJO/r71/Tltp3st7m9beonola3p7uvnzX+XyPpeiiikIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAK+AP+Ct/wC50X4H3HTy/GcXI6/dB4/Kvv8Ar4A/4LAfuvh38JLjp5XjODkdf9TIePyoA+/6KKKACiiigAooooAKKKKACiiigAooooAKKKKAOF8TfAj4aeNta/tjxD8PPCmvatwft+p6JbXM/HT946Fv1pPFPwJ+HvjXWPDura14N0e+1Tw7PFcaTetaqk1m0bB0COuCFDAHZnbkdK7uihaWt01+YPW9+unyCiiigAooooAKKKKACiiigAooooAK+AP+CcP/ACdN+2h/2Oa/+l2q19/18Af8E4f+Tpv20P8Asc1/9LtVoA+/6KKKACiiigAooooAK+FP+Cpnw11XT/Cfg348eEv3Xiz4a6lFcuVUnzbR5U+9jkhJQhI4GySUmvuusvxR4b03xl4a1bQNYtVvdJ1S0lsby2f7ssMiFHU/VWIoAw/g/wDFDSfjR8L/AAz440Nj/ZmuWMd5HGxBaFiMPExHG5HDIcd1NdhX59f8E3fFmp/BX4mfE39l/wAV3TG78MX02peHpLg7TcWbsC+wdMMrxThRz++lPY4/QWgAooooAKKKKACsK+8B+GdT8V2Hii88O6Td+JtPiaGz1qexie8to2DBkjmK70UhmyAQDuPrW7WF4y8eeGvh3pA1XxX4i0nwxpZkWH7drN7FaQeYc4TfIwXccHAzng0r21Hq9DdrAb4f+F28Yr4ubw3pDeK1g+yrrpsYvtwh5/difbv2cn5c45rif+Gsfgh/0WT4f/8AhUWP/wAdrrvA/wAUfBnxOgu5/B3i7QvFkNoypcSaHqUN6sLMCVDmJm2kgHAPXBqrdexLtsyDX/hB4D8V+JLbxDrfgnw7rGv2u3yNV1DSYJ7qLacrsldCy47YPFaFh4B8M6Xa63bWXhzSbO21yaW41WG3sYkTUJZBtlknAXErOOGZ8kjrW9RU9LdCru9zE0/wR4c0jwqnhmx0DS7Lw2kTQLo9vZRx2axkklBCF2BSScjGOTWP4X+Cvw98DxX8XhzwH4Z8PxahGYbxNL0e3thcoRgpIEQb1I7HIrs6Kb1u31EtEkuhyn/Cp/A//CO6T4f/AOEN8P8A9g6RcLeadpf9lwfZbKdSzLLDFs2xuCzEMoBBY8803TfhF4E0fxZP4p0/wV4dsfE05ZptattKgjvZC33i0wQOc98nmutop31v1DpboZ3iDw3pPi3SLjStc0uy1nS7gbZrHULdJ4JR6MjgqR9RXOaP8FPh54e8O6l4f0rwH4Z0zQdSUpfaXZ6PbxWt0p6iWJUCuP8AeBrtKKnv5j7eRhX3gPwzqnhJfCt54d0m78MLAlsNFnsYnshCgASMQldm1cDC4wMDFZtn8H/AWm2mgWtp4I8OWtt4fma50eGHSbdE02Vm3NJbqExCxbksmCTzXX1ix+NfD03iyXwsmvaY/ieK1+2yaKt5Gb1LcsFExh3bwmSBuxjJAzVXbfn/AJai6W6f0h3irwdoHjrR5NJ8S6HpviHSpCGex1W0juYGI6EpICpx9KZ4R8D+HPh/pI0vwv4f0vw3pisXFlpFlHawhj1OyNQufwrbopbbBvuFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXwB/wAFkv3XwS+HNx08rxnb8jr/AMe1wePyr7/r4A/4LSfuv2aPB1x08rxna8jr/wAeV6ePyoA+/wCiiigAooooAKKKKACikrzH4sftC+GPg3qWk2evC7Y6gsjK9pGriIKVGXBYHBycYz901Epxprmk7I6KGHq4qoqVGLlJ9Een0V5x4U/aG+HvjLy107xTYec/3YLp/s8hPoFk2kn6Zr0OOeOZQyMGVhkEHINOMozV4u4q1Crh5ctaDi/NWJKKSlqjAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACvgD/gnD/ydN+2h/2Oa/8Apdqtff8AXwB/wTh/5Om/bQ/7HNf/AEu1WgD7/ooooAKKKKACiiigAooooA+A/wDgpP4K1X4SeMfh3+1D4Mtt2t+Db2Ky1yGM7PtVg7FV3kDhT5kkLHk7bheyV9v+BfGuk/EjwXofirQbn7Xo2s2cV9aTYwWjkUMuR2YA4IPIIIPSmfEDwNpPxN8D674T163F1o+s2clldRkDOx1IJGejDOQexAPavh7/AIJw+PNT+DPjrx7+yx41uSdZ8KX0174dnk+UXdk58x1QdgQ63CjkkTydNlAH6A0UUUAFFFFABXxN/wAFchC37LumC42fZz4p08SeYcLtxLnPtivtmvij/grdClx+zDpMUih45PFenKyt0IIlBFRJXlTS/nh/6XE1p6Kb/uy/9JZpxeFv2FfLTdN8Ec4Gc6npv/xyvXvhVpfww8LfD/xNq3wA0jwbrIbdvtvC9/BHa3l3HHuSGWeESKjYcclSQHBxg1Wh/Ym+AjQoT8IvCJO0f8wqL0+lejfDv4W+EPhJo0+k+DPDmm+GNMmnN1LaaZbrDG8pVVLkDuQqjP8AsitXtJXs2c8fsu1/U8U+G/7dHg3xb+z34n+J/iK0k8H3HhSWaz8QeHbqYSXNleI21bcEqm9pCVCfKMsSOCpxR8Wftka/4B/Y+Hxy8SfDM6TcytbSQeF5NaJlNvPMkccsk32cbGKvv2bDxgEgk4+H/wBoWTw94y/am8TfGPQPCN3r/wAD/CGvaZa+OmtLhhaatfxs6tdLCBtlWHegbqGznhZS1fXP/BTLX9K8T/sF69rOmXUWo6Jfy6TdW9zbOCk0D3cDKyn0KkYqIy5qcaui5pQVuiu1r3tK91f7O2uq25eWq6W6Sk7999O149fPstHLq37eni+x8On4gWv7P3ii9+DSoLg+LhqVvHeNa55uk04jzTFj5gzMoKfMdor2T4gftVeAPh/8CLP4tTX8+q+F9QihfTV02Lfc38k3+qhijJH7wnIIYjbtbOMGuk1rxJ4Wtvgbe649zZ/8Iavh9rnz9y/ZzZ/Z8gg9NpTH518B/BX4qj4J/wDBP/4JWeq+ArHx94s8TeIZLXwjo+upH9nhnku5TBcM8inYF3Aqy4J3jBUZIqS1nTV7pxS7+82rdr6aaW3uYwd4U6j6p37aRvfvbv8AKx7j4u/bi+J/wt0ceLfH37NGv+HPh4rIZ9bt/Edne3dtG5AV5bNFDR8kAhnGCcE5r0j9or9sDQP2f/hz4D8dSWB13wv4o1azsmvI52iNrazxNL9qCCN2k2oufLAUnOMivnL9sC2/aV/4Zh+IGo/E3xp8NfC3h1dP2S6X4V025uZr4uyqtuZbpwIyzEDcgJHUVj/tCQx3X7GP7HMMyLLFJrvhRHRhkMpsyCDVQXNddpU18pN3v06dLPX0Zfw+8/5Zv5xV1br163/M9i8W/t3+Mvhta2nizxv+z54m8L/Ci4mij/4SifVbWW9t0kIEclxp6ZeEEkAhnyMgckgH1v48ftOaR8GdI8JDT9F1Dxv4m8YT/ZvDmg6QVWS/bYHLmRyFjjVWUs5zjcDjGccr/wAFGlDfsVfFIEZ/0CI8/wDXzFXnXxW+HvgP4tfDL9nPwxqvxBvvhx8UX0u2ufBesadHI0wnWyiMy8AKVICZUuhJCgHnByj7/NFdJR9Wne/ldcvb5D+Fxb6qfonHls+9ve11e252fhn9sTxdo3xE8L+EvjB8FdW+Fknim5+w6NqkOtW2tWctxjiKWSAL5RYkAZBznsASLekeKPCEn/BQrXNAi8EeT43j8CpdS+MP7WmbzbT7TGBafY8eWuGIbzAd3y4715B4n+Kv7Sn7Guv+EZfiV4l8M/F34e69rttoX26Gz+w6xA0wO1hHGqocBWPPmE4wSuQa6vQ8/wDD2DxPjr/wrGPH/gZDWkWuaElr8e3lTk7eu22jTt3vErpST7Rf3zSv6afJr7uq8Vftna3rPxC8QeDvgv8ACbVPjBf+G5jba1qMerW+k6bazjrCtzMGEkinIKgDpxnnHZfs8/tUaV8dNX8Q+FtQ8P6l4E+InhsqNY8K6xtM0KtjbLFIvyzRHIw4A6qcYZSfIP8AglZNBbfAnxZo9yVTxTpvjDUo9chf/XC5LLhn78qAM/7J9DUT3VtrX/BWKD+wmWV9K+HjQa88HIR2uC0aSEfxYeE4POMUoKzhF680b/Pk59PLpr63Kqf8vGtOWVvVc/J9/XS3oW/BX7fnin4uWesWvw1+BureNfE2jajc2epWcetwWVhaRxyskbNezxqrSyBd4iRGwOrV67+zP+09p/7RNp4lspvD2oeDPGXha8Fhr3hvU2V5LOVt20rIoAkRtrgNgZ2njGCfH/8Aglzbxx/Cb4kyIirJJ8QNWLsBy2BEBn8KX9l8Bf2+P2rwBgb9DP8A5KtU0PejCMtXKmpX87Qf3av+tBVNFOUek3H5czX6H2XRRRTGFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV8Df8FpI9/wCyn4eOM7PF9o30/wBEvB/WvvmvhH/gstH5n7JenNgfJ4ps25/64XI4/OgD7os5POs4HB3bo1bJ75FTVm+G5fO8O6XJyd9rE3zdeUFaVABRRRQAUUUUAQ3Unlwsa/NT9sTxkfE3xivLdZC8GmxJaKM8ZA3N/wCPOw/Cv0V8WapFo+jXd3O+yGCJpXb0VRkn8hX5DeL9el8SeKNU1Oc5mu7mSZ/95mLH9Sa8XNKlqah3P0jgjDc+LqYl7QVvm/8AgIqJOy9GIrrPCfxa8XeByP7D8QX+nRg58mKdvLP1T7p/EVxAb3pwkNfNxk4u8XY/ZqlOlXjy1YqS81c+oPCP7ePjnR9qaxbafr0X8TyReRKfoUwo/wC+TXtXhH9vbwbq2yPWtN1DQ5W6uu24hX8RhvySvz3ElPWT3rup4/EU/tX9T5fFcK5VitVT5H/ddvw2/A/XDwl8ZPBfjjy10XxLp97NJ92384JMf+2bYb9K7JZFbvX4xR3DJ0Yj8a7zwn8ePHngnYuk+KNQt4VOVgkl82IfSN8r+lejTzVf8vI/cfI4rgSW+FrX8pL9V/kfrHRXwL4R/b88Wabsj13SNP1mIdXi3W0p+pG5fySvbvCH7cvw/wBf2R6n9u0CduCbiHzYs+zJk/mor0KeOoVNpW9T4/FcM5rhNZUnJd46/wDB/A+jKK5rwx8SPDHjONX0TXtP1PcM7Le4VnH1XOQfqK6NXDdDXcmpK6PmpwnTlyzVn5jqKKKZAVxPxf8AiVD8KfAep+I5IBdtaeWEti+3zWaRVC57feznnGOhrtWOFNfHn7eXi8xaHofh+OTm5uGupFB/hRdq59iXP/fNc2JqexpSmuh7GT4NZhj6OGa0k9fRav8AA+lvhr8TtD+KnhuDWdEuRLDJ8ssLECWCTHKOOxH5EYIyCDXXV+T3wp+LGufCPxNFqujzHyzhbm0cnyriPP3WH54PUfnn9I/hH8YND+L3htNT0ibEiYS5s5CPNt3I+6w7g84YcHHsQObB4yOJVnpI9riDh2tk1T2kPepPZ9vJ/wCfU76ikpa9I+NCvgD/AIJw/wDJ037aH/Y5r/6XarX3/XwB/wAE4f8Ak6b9tD/sc1/9LtVoA+/6KKKACiiigAooooAKKKKACvgr/gpb8M9W8Bal4K/ab8CwhfFfgK7hj1VFyBd6ez7RvxyQGkaNscmOdiThBX3rWf4h8P6d4s0HUtE1izi1DSdStpLO7tJxlJoZFKujD0Kkj8aAMP4UfEzRPjJ8N/D3jbw7P9o0fWrRLqAnG5M8PG2OjowZGHZlIrrK/Oz9ifxDqX7Iv7S/jD9l3xXdSPoGoTSa34Jv7nP76NwWMYOMfOiNkDCiWCYDJev0ToAKKKKACvKv2kv2cvDn7UXw8j8HeKNQ1bTdNS+iv1n0WaOKcSRhgo3SRyDHzH+HPA5r1WipcVLf+ralKTjsfHv/AA7T0AcD45fG7/wro/8A5Grvfh7+xrp3w58J+M9Cs/in8TNUXxRZpZTX+sa5FdXVig35a1ZoNsTMHILFSeARggGvoWiqeqcXs9CVo010PNvhj+z14J+FPwYt/hdpOmC58JraSWlzDf7ZJL0SgiV5yFAZn3HJAA7AAAAfIf7a/wAB9J/Zz/4Jz+LvBmga1rmsaFBqljNZxa5PFM9mj30LGGNkjQ+WGJIDbiCx5r9Bax/Ffg/QfHmiTaN4l0TTfEWjzMrS6fq1pHdW8hVgylo5AVJDAEZHBANErylzPq4387NP/hiqdoWVtFe3zVv+HPmKx/4J0/DTWLHT4rnXvHLeCXWO6b4fr4kmHh/zDhyRb43KN5LYDgA9ABxXsfxk/Zp8A/HL4c2PgnxFpBg0bTXjl0w6XJ9ll02SNSkbwMvCFVJAGCuOxr1CONIY1jjVUjUBVVRgADoAKdVTfNddL3/y+a6GVNOCV90rf5/f17nyvJ/wTp+H2uaLe6f408XfEL4lCS3lt7Kbxl4ke/OmGSNozLbR7FiWRQxKs6NtIBHSu28SfsheEfFXwu+GfgS/1jxA+leAL6xv9LuVuIBczPaKVhWdvJ2su04O1VJwORXuVFLmf4p/NbP5Ff8ABXye6OJ+NXwl0f47fC/X/Amv3N9aaRrUKw3E2muiXCqHVwUZ0dQcqOqnjNct8Sv2VfAPxa+GPhzwR4ktby5tPDkUCaRqlvcmDULKSKMRpNHMgGHwoJ42kgHbwMev0VPKtV3t+G33X0Ku7p9r/ja/32R83+Bf2EfBfhfxlo/ijxF4t8efFHVNFl+0aR/wnviBtSh06XtJDGERd3AwWDYIBGCAa9Es/gB4esv2hb74xpeamfE95oS+H5LRpY/sQtxKsgYJ5e/flBzvxjPFemUVfM9PK/4qz+9OxNlr5/pqvxPnn4ofsP8Agf4ieO7zxrpOveMPhn4t1BQmo6t4C1ptMl1BR084bWVjx1CgnuTXZ/An9mrwN+ztp+pReE7G5fUtWlE+q63qly13qGoyjPzzTNyeSTgALlmOMkk+p0VMfcVo6L+vw8hy953keafAb4A+Hv2ePDmtaL4cvNTvbXVtYuNanfVJY5HWabbvVSkaAINowCCevJpPAfwA8PfD34vfEL4jadeanNrfjc2h1G3upY2tovs8ZjTyVWMMuQedzNz0xXplFEfdtborfLRW/BA9U0+rv873v97CiiigAopKWgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAK+G/+CxUPmfshI3/ADz8R2Tf+OTD+tfclfE3/BX6PzP2ObxsD5NcsW5+rjj86APr3wNN9o8E+H5f+emn27c+8amtyuY+F8nnfDPwlJyd+kWjc9eYUrp6ACiiigAooprfdNAHh/7Wni4eF/g7rzq+yW6jFomDyd5ww/743/lX5eGbexJ6k5Nfor+2J8Ptf+JHh/T7HSJYEht5mnmjmcqznAC7eMHgv1I618Ja98JfFPh1m+1aXNtXq6ruX/voZH6185mMakql7aI/YeEK+FoYRwdRe0k27X17L/P5nMh/enCQ1DNBPb/62J09yOPzpiyV4tj9IUi2JKcHFVRJThIKVi1ItB/enCQ1VD+9OEhpWLUi2JKeslUxJTw1KxakaFvfS28ivFI0bqcqynBBHQivSPCP7SXxE8F7FsPFF7JAvSC8f7RHj0AkDYH0xXlIf3pwkq4znTd4Oxz18Nh8VHlr01JeaufYXhH/AIKCaxahI/Efh20v1HBnsZGgf6lTuBP02ivbPCf7aXw28SbEub+60Odv4NQtzjP+8m4Ae5I/pX5piSniSvQp5jXhu7+p8piuEMrxGsIuD8n+juj9g9I8baF4osTcaNq9jqkOMl7O4SUD67ScfjX56/teeLP+Ek+MF5bo+6HTYY7VfTON7fq5H4V4lY6vd6fOk1tcS28y/dkjcqw+hHSl1DVLnVryW7vLiS5uZTukmmcs7nuSTyTTxOPeIpcnLYyyXhaOUY3617TmVmlpZpv/AIAV1Xw3+JOt/C3xLBrOh3JhmT5ZImyY50zyjrnlT+nBGCAa48SGnCSvKjJwalHRn3lalTxFN0qqvF7pn6nfBP436L8ZPDq3lk62+owqovNPdsvAx7+6nBw38iCK9Lr8h/A/jzV/h74itda0S7a1vbc8Ecq6nqjDup7j/wDXX6PfAX9oDRvjPomYitnrdsgN3p7Nyvben95Ce/UdD1GfrMHjViFyT0l+Z+B8RcN1Mqm69D3qL/8AJfJ+XZ/f5+t18Af8E4f+Tpv20P8Asc1/9LtVr7+BzXwD/wAE4f8Ak6b9tD/sc1/9LtVr1T4U+/6KKKACiiigAooooAKKKKACiiigD4z/AOCmHwB1Dx38MdN+KXgxGtviP8N511mxurdR50lrGwklQf3jGVWZQc/ccAZevcf2Vvj9p37S/wADvDfjqxMUV3dQ+RqdnEc/ZL2MATRYySBu+Zc8lHQ969aZQykEZB4INfm38MZG/wCCff7dWofDy4zY/B34put3ockpIgsb3JCxqTwuHbySBztktmY4FAH6S0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFNkbapNOpkq7kIoA+X/wBoz45eOfhL4utTpU1lPol9DuijubbcY5FwHXIIJHKtz/eI7V53Zft1+MY/+PrRdFnH/TNJUP6yGvW/2nvAreKfB90sce+6tv8ASYOOdyjlR9VyPrivg2R9jEdxX6JkmGwOPwtqtNc8dH+jPis1r4vB1705vllqv1PrSz/b4vY8favCEEvr5V+yfzjat2z/AG+NFfb9r8MXsPr5NykmPzC18UPNULTV7E8gy6W0LfNnmxzjGr7V/kj77sv26vAdxgT2OtWrdy0ETL+Ykz+lbtj+2T8MrvHmatc2n/XazkOP++A1fnC0tRNLXFLhvBPZyXz/AOAdUc8xS3SfyP1Esf2m/hpqAUxeK7VQ3Tzo5Yvz3KMV6Hout2PiLTYNQ026jvLKdd0U8LZVxnGQfwr8w/gV8L3+IniiBrpHGk27h52HG4dkB9T+gyfSv0u8L26Wel21vDEsEEMaxxxRjCooGAAOwAr43NcHhsDUVKjJyl1vbT/gn0+X4mvioOpVikunmblFFFeEesFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFfGH/BXKHzP2Mdab/nnq1g3/kXH9a+z6+O/wDgrNHv/Yp8UHGdmoae30/0lB/WgD6T+Dc32j4Q+Bpf+emhWLc+9uhrsa4T4CSed8C/h04O7d4c05snvm1jru6ACiiigApDyMUtFAGJrPh+LU0Idc1wurfC2CfcVQflXqtNKhuooA+Z/E/7P+m6rvNzplvOx6uYwH/76HNeP+Kv2R9JuN7WqTWL9tp3qPwPJ/OvvOS1jk6qKo3OgW9xnKCsJ0KVT4onp4bM8bg/4FVryvp92x+YfiL9lvX9NZ2sJo7tR0U/Ix/A8D86841v4c+I/D2TeaZPGg/j2Hb+fT9a/WbUPANpc5/dj8q5TVPhTFJkrH+lcE8tpS+F2Pq8NxljqWleKmvuf4afgflHIkkBxJG0Z/2hikWT3r9E/FH7OukaoH+0aRA5PV0TYx/4EuDXjnij9kSxkLtZST2bdQrKHUflg/nmvPqZbVj8LufWYXjLA1dK0XB/evw1/A+UhJThIK9Y8QfszeJtJZ2tPLvUHICuA2PocfpmvPNY8E67oDEX2mzw843MhAP0z1/CvPnQqU/ii0fWYbNMHi/4FVS+ev3bmYH96eJDVVt8TbXVkPowxSrJ71hY9RSLYkpwaqgkpwcfSlYtSLYc+tOElVQ/vThJSsWpFtZKeJKpiQU4NSsUpFwSVs+E/F2qeCddtNY0a9ksb+2ffHLGefQgjoQRkEHgg4Nc4HP1p4koV4u6CajVi4TV090fp1+zv+0dpnxk0kW1wYrHxLbpm5sgcLIBx5keTyvqOq55yME/Nn/BOH/k6b9tD/sc1/8AS7Va+avD/iO/8Mava6npl1JZ31s4kimibaykV9Gf8E4FTQ/jN8cNW1PVbaS/8d3trrEEGNjtKJb2W5UDphTcKRg5wTx8pNfU4PGqt7lT4vzPw7iPhmWXt4rCK9Lqusf+B+R+hNFIrBuRS165+fBRRRQAUUUUAFFFFABRRRQAV87/ALdP7MUP7UXwJ1LRbSJB4v0onUvD90WCMt0in90W4wsq5Q5OASjH7gr6IooA+Xf+CfH7T0/7RnwVS38RSNF8QvCsg0nX7a4Gyd3UYjuGQ8jeFIbIH7xJBgACvqKvzg/am0e+/YV/a00T9ovw3Zyy/D/xdL/ZfjPTbVfuzPy0wGMAvtWUessTgsBLiv0R0LXNP8TaLYaxpN5DqGl6hbx3Vrd27bo5onUMjqe4KkEfWgC9RRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFVNR1S00m1kury5itLaMbnmncIij1JPAr59+Jf7aXhTwss1t4fRvEWoKSodCY7ZT67yMt/wABGD6iuvD4WvipctGDZz1sRSw65qsrH0U8qxqSxAArx34k/tUeB/h+skC3/wDbWorkfZdOIkAPoz52r9Mk+1fFXxI/aO8a/EozQ32qNaadJ/y4Wf7qLHocct/wImvLZJyxySSa+zwfDO0sXL5L/M+XxOe/Zw8fm/8AI9v+KX7Vnin4hNLb2oj0LTmJAhtSTIR6NIeT/wAB2/SvEprhpGLMck1XaWoWlr7HD4ahhI8lGKij5mtXq4iXNVlcnaWoWlqBpqheat3IyUSw01bPgvwreeNdet9Os0LNIwDN2UdyfbFYFlbzaleR20Cl5JG2gAZr7q/Zx+Ca+FtLimuIt1/OA0rEfdH93/H3+grw80zGOBo3XxPZfr8j1sBgni6tn8K3PQ/gt8LbXwnotrawx4WMZZyOXbuxr2+2gEEYUCqulacllbqqjGBWhX5ROcqknOTu2focYqEVGKskFFFFQUFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFfI3/BViPzP2H/ABw2B8lzprc/9f0A4/OvrmvlD/gqZHv/AGF/iMcZ2PpjfT/iZWo/rQB7R+zbL537Ovwsk5O/wrpTfN15tIq9Hry79liTzv2YfhC4O7d4P0dsnvmyhr1GgAooooAKKKKACiiigAooooAKaY1bqKdRQBXksopOqg/hWddeG7a4BzGv5Vs0UAcPqHw9tbgHEYrkdY+EsUyuBGGVuCCODXstNaNW6igD5J8U/s0aLqW8yaTEpPO6EGP8eOD+NeQeJv2Q4AXbT7qa3bssqBh+Yxj8jX6HS6fFL1UGs268L2txnMa/lXNPDUanxRPaw2dZhhP4VZ27PVfc7n5Za/8As4+K9G3NDEl7Gv8AzxbJ/I4P5CuA1Lwzq2iy+XeWE8D/AN10IP5Hmv1p1L4cWtwDiMflXm3xA+HVlpOh317dwpJa28LzSK6gjaqknr7A159TLab1jKx9ZhOM8XFqNemp+mj/AFX5H5mFirYYFT6EYpyyVLr18L3WLqXCqC5AVRhR7D2qiGr52x+vRm7alwSU4SD1xVMP708SUrGikWxIfrThJVQSU8SUrFKRaEgq9pOsXeh6hb31jcSWt1A4kjliYqysDkEEdCDVG3tLi6IEcDvnpgda1/BvhK98eapqOnaJJBfXmmsqX0MMys1qzFgFkGflOUfg8/KaqNOcn7iMK+Kw9GDeImkvNpfmfoD+zD+1Va/E63h0DxDNHa+J41wknCJegDqB0D+qjg8kdwPpRWDDIr83fh/+yrrN1qFvcXetDS5I2V1e1VnkUg5BH3cEeoJr9A/BNvdWPh+ytby+m1O5hiCPeTqqvKR/EwUAZr63CSrOFqy+Z+B59Ry2Ffny6pdPda2Xo9reXQ6Giiiu4+YCiiigAooooAKKKKACiiigDlfil8NNC+MXw917wX4ltftei6zatazoMbkz92RCQcOjBWU9mUHtXxJ+wD8Std+AHxS8S/sofEe63aho0st54R1KX5UvrRsyGJOeQVJmUclf3yEjywtfoLXyJ/wUK/Zb1L4xeDdM+IfgLzLL4t+BHGo6Pc2q/vrqONxI1uOOXDDfGCD84K8CQmgD67orwT9i79qTTv2rPg3Z+IQIbLxRYEWOv6XGSDbXSj74U8iOQDevXGSuSUave6ACiiigAooooAKKKKACiiigAoopCwXqaAFpM1xPj74y+Evhrbs2uaxBbzhd62kZ3zuPZBz17nA96+V/iT+3Nq2peZa+EdPTSoOR9suwJJyOxC/dU/8AfVephMsxWNf7qGnd6I8/EY/D4X+JLXt1PsLxV420PwVpzX2t6nbabar/AB3EgBY+ijqx9gCa+ZviV+3RZWfm2vg7TTeS9Pt1+CsYPqsYOT+JH0NfIHiPxdq/ivUJL7V9RuNRupPvS3Ehdvpk9vbpWI0tfbYPhuhRtLEPmfbZHyuJzyrU92guVfidn46+LXin4i3Xna9rFxeqrFkhLbYk/wB1BhR9QM1xzTe9QNLULTV9XCMKMeSmrLyPn5SnUlzTd2TtLUTS1A0pJwOTW/4b8Aa54smC2VlIyZwZCMAfUngfjWdStGnHmm7LzKhTlN8sVdmC01XtI8P6l4guFhsrWSZm6bVJ/GvoXwH+y2rOkuqubl/+eUedv4kj+QH1r6J8K/Be00qzWO3tI7dAOiKBn3J7n618pi+IaNP3aC5n+B9Fh8lq1Nar5V+J+d/irw3e+E75bS+QpKVDEcemex+lYW4swUDJJwAK+uf2tfhQbfQ4tXtYSZrVtkhUfwE8H8+P+B15B+z38IJvH2uR315Ef7NgYE5z859B9f0H1FduHzOFTB/Wqjtbf1/4PQ5a2AnTxP1eGt9vQ9N/Zd+CTzyQ6/qMOXY5t0Yf+Pf4fn6V90eGdDTTbVAFAOKxPAfhGLSbKJVjVFVQAoGAB6V3SqFUAV+c4zFzxlZ1Z/LyR9rhcPHC01Tj/wAOKOKWiiuI6zF8a+KIfA/g/XPEVxZ3eoW+k2U19La2CK9xKkSF2WNWZQWIU4BIye9YPwT+MGhfHr4X6D488NLdR6NrETSwR3qIk8e12jZHCMyhgyMDhj0612lxbx3VvLBMgkikUo6MMhlIwQfwr4t/YD16D4N/Dn41fD/WZRBbfDDxNqLAu33dOdTPE/0IWRvxqeZR5+fZR5vudn/6UvuZTi2ocu7lb702vyf3nrWg/tq/D7xH+01qXwMtYtWXxbYiQG9khiFhNJHEsrxRuJS5dVY5BQDKNz0z2P7Qnx+8Ofs1/DmXxl4nttRvrBbqCyjs9Jijlup5ZW2qsau6KT1J+YcKevSvzm0/wxqHgH9nf4W/tO30Jh8QSfEibxdrEhyWGm6jN5Ei/QokJHb5zX03+2JGvxd/aO/Zv+FsP+k6dLrEvjDUwpyv2ezTMW7/AGXJkX8a0jF2pwlpLmUZfdGUvui33+FvUiUopzlHWPK3Hz1lFfe0n/28kfYlrObq1hmMTwmRA/lyY3JkZwcEjI9jUtFFJ7gr21CiiikMKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAK+W/+CnkfmfsM/E4Y3fu9Pb8tRtT/SvqSvmX/gpVH5n7EPxRGN3+i2rfle25/pQB3/7Icnmfsp/B053f8UhpK/laRD+let14z+xjJ5n7JfwgOd3/ABS2nr+UCD+lezUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAhr59/bJ8XJ4W+DmsYYLNebbVOeu45YfiivX0DIcKa+PP21vCXib4kTaLoeiWMktnFvuLi4OAisSFUZJAyAG4HOGrmxLkqUuVXZ7OTwpzx9L2skop3bei01/4B+fHnFiSTkmnCQV9C+HP2QdRuGQ6leqnqkQL/AOH8zXrfhX9krQ7Eo0lpLduP4pTgf+O4P5k18/DA1p7q3qfrGI4ny7D6KfM/7q/V2X4nxXa6beXjKIbeSTdwPl4NdnoPwZ8V67tMWmSxof4pF2j82wD+Br798N/Amw0sL9m0+C2944wCfqeprvdN+FsEOCyCu6GWL7cvuPmcRxpU2w1K3nJ3/BW/M+D/AA7+ydql5tbULxIgf4YgXP07fzNeseF/2TdGs9jS2012/rK20f8AjuD+Zr6/sfBNpbgfu1/Ktm30W3hAxGo/Cu6GDoQ2jf1PmMTxFmeJ0dVxX93T8tfxPA/DfwIsNLC/ZtOgtv8AajiAJ+p6mvl3/gnr4Oi1L9pL9rS2kXIsvFaRj/wM1Mf+y1+lKWsadFFfAv8AwThUf8NTftof9jmv/pdqtdiSirI+enOdR803d+Z9sab4NtrPBCDIrore3WBQAOKmopkBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAH5t/tGeFda/4J+/tKRftBeCtPuL34W+K7gWvjTQ7Q8QTSOSZgpOBuYl0JwBJuQlVlAP6F+DfGGjfEDwrpXiTw9qEOqaJqlul1aXkByssbDIPqD2IPIIIIBFJ4y8HaL8QvCuq+GvEWnw6roeqW72t3ZzjKSRsMEeoPcEcggEEEA1+d3wL8Y6v/AME4/wBoiT4I+PNQluPg54suXuvCPiK9ICWcrMAUkfICrlgkvZXKSYVZGNAH6V0UUUAFFFFABRRVe8v7fT7d57maOCGMZeSRgqqPUk9KALFNaQL1NfP3xK/bK8H+D/OttGLeJNQXgfZ22W4PvIRz/wABBHvXyj8Sv2nPG3xGaWGbUW0zTXyPsNgTEhU8YY53Px2Ykewr6HB5Hi8X7zXLHu/8jxsTm2Gw+ifM/L/M+1viR+034I+HKywzakuqaihK/YtPIkYN6M33V+hOfavlH4lftleMPGHn2ujsvhvTn4AtWJnI95eCP+Aha+fJLgscscmoWlr7bB5FhMLaUlzy8/8AI+UxObYnEaRfKvL/ADLt9qVxfzvNczPPK53M8jFix9ST1NU2lqBpaiab3r6C6irI8ezerJ2lqFpvei2t7i/lEdvE0rk4AUV6X4N/Z/17xI0cl2hsbduf3gO7/vnr/L61xYjF0cNHmqySR1UcPUrvlpxueYKzzNtRWdj2UZNdr4R+D/iDxbIjJbNb2zf8tpOBj29fwzX1L8Pv2bNL0fY/2P7TN18ycZ/IdP6+9e7+H/hnBaqpeMflXx2L4j3jho/N/wCR9Lhsk+1Xl8l/mfMnw9/ZdsbNopbyNr+fvvGE/Lv+PHtX0N4X+E9vYwxoIEjReiquAPwr03T/AA/b2agKi/lWokKp0FfIYjFVsVLmrSbPpaOHpYdctKNjB0zwrbWSjEYyPattLVI1wABU1Fcp0HnvxI8DQeLNJu7GdN0NzG0T7eoBGMj3rE+GfwpsvBmnW1jaw7IYFxkjlj3Y+5r1mSFZOoojhWPoKv2kuTkvpvYjljzc9tRLeFYYwoFS0UVBYUUUUAFfl7+3feax8I/j58QNA8PwMsvx28NabpNq0YOG1CO8jtZFPpm2kbn1cetfqFWB4g+H/hfxZq2karrnhvSNZ1TR5TNpt7qFjFPNYyEqS8LupaNsqpypB+UelTypzi5arqu6aaa/rsUpOMZKO/Tyaaaf4HnHxa+Ath4m/ZP134T6fCv2ZfDX9laeu3hZIYQLdsezxofwr5U/4Jw+Irv9oL4rat8TdUjmdvCXgvR/BFvNOCC9wE828bn+Leo59H96/RGsLwn4D8NeAba7t/DHh3SfDlveXDXdzFpNjFapPMwAaVxGoDOQBljycCtIyftZ1ZauX5+8r/dKS+4z5V7KNKOy/L3X+cY/K5u0UUVJQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFfOH/BRaHz/wBin4qL6afE35XMJ/pX0fXz3/wUEj8z9jP4rjG7/iUFvylQ/wBKANP9h6bz/wBkL4Rt6eHLRfyQD+le414J+wXJ5n7HPwmOd3/EjiX8iw/pXvdABRRWH4u8c+G/AGl/2l4o8QaX4b07O37Zq97Haw59N8jAZ/Gle249zcorm/BfxL8IfEm1mufCPirRPFNtC22WbRdRhvEQ+jGNmAP1rpKrVbiCiiikAUUUUAFFFVY9Ts5tQnsI7uB76CNJpbVZFMsaOWCMy5yAxRwCeDtOOhoAtUUVV1TVLLQ9Nu9R1K8t9P0+0iae4u7qVYooY1BLO7sQFUAEkk4AFLbVjV3oi1RWX4Z8VaL410O21nw9q9hr2j3QJg1DTLlLm3lAYqdkiEq2CCOD1BFO8ReJNI8H6Ldaxr2q2WiaRaLvuNQ1G4S3ghXIGXkchVGSBknvTfu7iXvbGlRVXStVstd0y01LTby31DTryJZ7a7tZVlimjYBldHUkMpBBBBwQatU2mnZhvqhrLuUiue1bwzHqTZcZ/CrWh+NPD3ijUNWsNG13TNWvtIm+zaja2N5HNLZS8/u5lViY24Pytg8GtikBy9n4JtLc58tfyrYt9Ft4QMRgVo0UAQpbJH0UVLtA7UtFABRRRQAV8Af8E4f+Tpv20P8Asc1/9LtVr7/r4A/4Jw/8nTftof8AY5r/AOl2q0Aff9FFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXk37Tf7Nvhf8Aak+Ft74P8SxmJ8m407U4hmWwugpCSr6jkhlPDKSODgj1migD4G/Yv/aT8U/CX4iSfsyfHSVbTxZpO238Ma9OxEOr2o4hiEhxvJUfu2PLYMbYkXDffNfOv7aH7H+kftW+A4Y4Z10Tx5ou648P68hKmCXIPlSFefLYqORypAYdCG8y/Yx/bO1rXPFFx8D/AI4W7eHPjHop+zRTXYCJrSKMhlI+UylcN8vyyKd69wAD7XooooAiuJPLjJr4A/bE1LxHb/ECSC61e7utCuFWe0tmfEUXG1l2jAJBB5xnDDmvv+4TzI2HtXy3+1h8PW8QeFZ7qKPddWOZ0452/wAY/IZ/4CK9rJ8RHDYyEprR6el+p5WZ0ZV8NJReq1Php5s9TUTS1DK5RircEHBqBpvSv11yPzhRJ2mqFpq2vD/gjWvFE4jsbKWQcZbbwPr6fjivcfAf7LbTPFNq7tM3Uwx9PxP+A/GvJxeZYbCL97LXt1PRw+Br4n+HHTv0Pn/S9E1DXLhIbK1knd+m1Sc17B4J/Zm1LVnSXVpDboefKj+Zj/Qfr9K+sPBPwTs9HhWO3s47dO+1eT9T1P416ro3ge2sVX92M/Svi8XxDWq+7h1yrv1/yPqMPktKnrWfM/wPC/APwA07Q1jNtYqjgY81huc/j2/CvZND+HltZqpaMZ+ldrb6fFbqAqgfhVkKF6V8tUqTqy5qju/M+ghCNNcsFZFGz0mG1UBUAq6qhegp1FZlhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXgn7eUXnfsdfFpcZxoUzfkQf6V73XiH7b0fmfsh/F0Y3f8AFOXjflGT/SgDJ/4J9S+d+xj8KGznGk7enpLIP6V9C183/wDBOaTzP2KfhWc7v+JfMv5XMw/pX0hQBi+NvFVp4F8G694kv8my0ewn1Cfb18uKNnbH4Ka+Kf2N/gNpP7UHhpvj/wDGzTbfx34m8UXE7aVpesoLjTtI09JWjjhht3ynJQnLA8YP3i5b7B+MHgtviR8J/GXhRGEcmt6Pd6cjk4CtLCyKfwLCvnj/AIJj+PLTWv2YtK8GXBWy8V+CLm50XWdJlO2e1kWeRlLKeQCrYz0yrDsaKdnKo+qSt6Nvma/8lXo/MdS6hBLZt3+SXKvT4n6pdiT4w/sL6cnibwv45+BEWi/Cf4gaNfRNLPYQNa6ffWWf3sE1vANrZ4/hG7GCehX0v9oX9p3R/wBn+Hw9psmj6l4v8b+JJWt9F8LaGge5vZFA3tk8JGuRlznAPQ4OE/am/ac0j9mDwRp2sXemyeI9a1XUYdN0vw/aTiO6vpHcBvL+Vs7VOenJKrkbhXiHjK8Fj/wVC+F2oeIofsEGqeAri10lblgVS+EsjSxK3TeEJBx13D1FKN58tNPTmf38vM0vWy9L33CVop1JLVRX3c3Ld+l38lbY6rTP22vEPg3xl4f0P43fB3VPhDa+IrpbLStc/tm31iwe4b7sU8sIHks3bOe5OACR0Xx+/bIsfgF8XvCngW78I6n4juPEemzXVj/YzGW6mulkCR2scGzBLkkl2kUKFJOa4b/gq5fabH+yDq+nXOyTWNS1TT7fR7cDMsl0LhGxGOpby1k6ds+tY/xKspf+HiX7NMeoqJbyDwrqRkL8kSiCQE/XOaIfvJRjt7zT80qbl96fy203RNT93Fy392/o+dL7nf1312t2Og/tqeJ/D/xS8LeDfjB8GtU+FS+LLn7FoWrf21batbXFwSAsUphUeSzEqAMscsMgDLDq/jV+1RfeA/iVZ/DTwD8PdS+KPxFm0/8AtaXSbW+h0+2tLTfsEk11LlUJbgLg54yRkZ80/wCCkAHnfs7nHP8AwtDSufwkqb47fB/Q/i5+00bv4Z/GG9+GPx70PREF7DbWbXMN1ppfKCWJ9qONzr0ZgPlyhIBAveUf8Uk7btKCknr2b1t0RT0b9E9druTX6aebO++Dv7V2q+OPiJqXw38cfDPVfhr8RrbTTq1vpN1fw39pe2+duYruIBCd3BGMDB5JBA+aP2MPiJ8T7/8AbX+Op1D4SnTzrWoaaPEufEttL/wjWy3m8kcL/pfmf9Msbcc16d8Kfjn8c/hT+0f4R+DHxsk8NeME8VWd1c6T4o8OxtBPmBHdvtEW1VGQmPlRQCwwzc4l/ZG/5PW/a5/7COi/+iJ61pfxOdapwl6O04p+a8/NaWu0RUv7KUXo+aP4r+mvWzufZdQX1jBqdjcWd1Es9rcRtFLFIMq6MCGUjuCCanorKSUk09i02ndHxT/wT1luPhD4v+L/AOz1qcshfwbrLanonnHmTS7r50K+uDtY+8xq3/wUEubj4ra98KP2fdMlZZvHWtLe6yY85i0q0IklJx03EZHqYsU/9qG1/wCFH/tY/Bv4226+TpGrzHwN4ldRgeVcEtayOegCyZJJ/uKKk/ZghPxy/as+MHxtnBm0fSJB4F8Muw+UwwENdSp6hpcYb0ZhTpv2vsnLXl+L/ty1v/Ar02/V/JT/AHbqOOnN8P8A2/e/3Wnb0Xz6z4hftZP4R+IUvwn+Efwz1H4qeMNDtYmv9P0+9h03T9KhKjy45bqUFEcrjCY6cZyCK1vgf+1tH8SPiHqHw18a+C9T+F/xOsrX7cfD+pzx3UV1b5wZba5jASYDvgDvjO1seYfsEzQ6f8aP2o9H1IiPxWPHMt5NHL/rns5Nxt29SmNxHYbh60z9ou6ttV/4KKfs06fo7LLr+n2urXWp+Ty8Vk8BCeZjopKygZ7k+tOm3KVJT19ort9rxctPJdb30u9wqJRVXl09ndLzs7a+vS3dblv9hv8A5OB/aw/7HOP/ANBmr7Jr42/Yb/5OB/aw/wCxzj/9Bmr7JqY/wqX+CH/pERf8vKv+Of8A6XIKKKKYwooooAKKKKACvgD/AIJw/wDJ037aH/Y5r/6XarX3/XwB/wAE4f8Ak6b9tD/sc1/9LtVoA+/6KKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAr5s/bO/Yx0X9qbwvb31jcL4c+JOijzdC8SQko6Op3LDKy/MYy3II+aNjuX+JW+k6KAPiP9jv8AbY1a/wDE0nwR+O8X/CLfF/SZBZwXN9tji1ocBCrfdMzDBG35ZQQycnFfblfP37Xf7G3hL9rLwnHDqB/sPxhpyk6P4mtY8z2rZJCPjBkiLclcjBJKkHk+Cfs1ftleL/g78QIvgP8AtND+yfFMO2LRPGVw+bXVoslY/NmIAYtjCzHG45WQLICWAPvuuS8caKuo6fKpQMCMEEV11QXVuLiMqRnNAH5k+L/2fNdbx9qNlp9o8emiTMdxIMJtPIGe+AcHGTkGvS/h/wDsuWdq0Ut+rX0+c4IKoP6n9B7V9hXPge3uLnzGjB59K19P8O29moCoBXu1s6xdaCp81kl03fzPJpZXhqc3Plu/PZHl3hX4SW+nwxotukMa9ERQAPwFejaX4StrFRiNfyroY4VjGAKfXhttu7PV20RDDaxwgBVAqXpS0UhhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFeNftmQ+f+yZ8YF9PCuot+Vu5/pXsteS/tcx+Z+yr8Yxjd/wAUfq7flZyn+lAHn3/BNObz/wBiD4XN6W12v5X1wP6V9N18s/8ABMGTzP2F/hic7vk1Ffy1K6H9K+pqACvAfi1+xL8Pfip42fxrb3PiHwD44lQRTeJfBOqvpl7Oo7SEBkY9PmK7iAATgCvfqKVle47u1j56+F37Dnw9+HHji38balqHib4keNLVdlp4g8eau2p3VqvOBHlVRSMnDbdwycEZNd58cv2efBH7RHhy20jxlpslwbKb7Tp+oWczW95YTdpIZV5VuBxyDgZBwK9Jopy95JPoKPuttbs+b/AP7B/gTwl420vxb4h8ReNfilr2jv5mk3Pj7XW1Mac396FNqKDkAgsGwQCMEA16L4m+APh7xX8cvB/xVu7zU4/EPheyubCztoZYxaSRzqyuZFMZcsAxxtdR0yDXpdFO70fa9vmmn96bFZWa7/pqeZ/Gz4AeHvjw3gw6/eanZ/8ACK69b+IbL+zZY08y4hzsWXfG+YzuOQu0+4rA+Of7I/gj48eINL8S391r3hXxnpcRt7PxV4T1JtP1GKIkkx+YAVZfmb7ykjc2CMnPtdFTbS3nf52t+SsVd/hb5b/meIfBf9kPwb8GfFlx4tGq+JvHHjWa3+x/8JN401ZtSv47fOfKRiFVFz6LnkjOKjn/AGRPC8f7QE3xd0fxL4u8Ma9eyQy6rpmjaqIdM1dol2J9qgKN5g28YDAdwASSfc6Kq75lLqtv6/rUmys49HueU/Dz9nDw18NfjH8QPiVpl9qs+u+NjAdRt7uaJraLyhhfJVY1Zc553M34V6tRRSXuxUFstEPduXV7nCfG74NeH/j98M9Y8DeJjdR6TqQjLT2Eix3EDpIsiSRsysFZWUEEgj2o+CPwa8PfAD4ZaN4F8Li5bSNMVwk166vcTO7s7ySMqqCzMxJIAHtXd0UL3b267g9bX6Hhfxn/AGOfA/xm8X2/jE3/AIi8DeOIYRb/APCUeC9UbTdQkhH/ACzdwGVhjAyVzgAZwMVf+Bn7J/gX4B6rqmu6T/a3iHxfqqCPUPFXie/a/wBTukBBCtKwAA4XIVVztXOcDHstFEfc+HT/AIO/39Ql73xf1bb7uh5n8K/gD4e+EPjD4h+I9GvNTub7xxqY1XUY76WN4opQGG2ELGpVfnPDFj05qp+zr+zf4Z/Zl8L63oXhe+1a/tNX1ebWZ31eaKSRZpURWVTHGgCYjXAIJ5PJr1eiiPu7dlH5K1l+C+4N7+bv89dfxf3hRRRQAUUUUAFFFFABXwB/wTh/5Om/bQ/7HNf/AEu1Wvv+vgD/AIJw/wDJ037aH/Y5r/6XarQB9/0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV5R+0b+zP4H/ah8CS+GvGWn7ymXsdUtgq3lhKcfPE5BxnAypyrADI4GPV6KAPzT+H3x4+Jv/BOPxbpnw0+OjXPi74SXT/Z/D/jq1jeR7OMDiNhyxRR1hYl0GdhdAq1+jXhvxJpXjDQbHW9D1G11fSL6JZ7W+s5RLDNGejKw4Iqj49+H/h34o+E9R8MeLNHtdd0HUI/LubG8TcjjqCD1VgcEMpDKQCCCAa/PHXfhf8AGX/gmdrl14n+Gc158TfgPLO0+peErlma60tSctIpCnbgf8tkGDj96nyhqAP0tpa8n/Zz/ac8B/tQeC4/EHgvUxLIgC32k3JVL2wkP8MsYJwPRhlWwcE4OPWKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAry/8Aami8/wDZj+L0eN2/wfrC49c2Uwr1CvOv2jo/O/Z5+KCY3bvC2qLg982ktAHin/BLKXzP2F/h0uc+W+pr06f8TG5P9a+sK+RP+CUsm/8AYh8FDOdl1qS/T/TZj/WvrugDP8QyvDoGpyRu0ciW0rKynBBCHBB9a+Yv+CYvjTxB4+/ZE8O6z4n13UvEery318kmoateSXVw6rcOFBkkJYgAADngV9N+Jv8AkW9V/wCvSX/0A1+YX/BP79kfVvi5+zNofiS0+OXxO8Dw3F5eRjRvDGuPa2UWyZlLLGOhbGT6k1NK/tKq/ux/9KYVfgp/4n/6SfSf/BSLxx4j8C+CPhbP4b8Qap4fnvPHenWdzLpV7JbNPAyy7onKMCyHAyp4OBxX0x8QviR4X+FPhe58ReMNdsfDuiW+BJeX8ojTceir3Zj2VQSewr81P20/2X9T+Cel/C3Wr34x/ET4hRXHjjTbUab4u1lry2iJ3t5qoejjbjPozetd/wDto654o8Rft3fCjwtpnw8T4rWeh6BNr9r4RutWg063urpnlQztJODG3liJCFIJ4PvTj8KinvN/K0Iv8l971tqxy+Jya0UF13vOS/Nr7uuiPqX4Q/tofBX48eIG0LwR4+sdW1nBKWE0E9nNLgEny0njQyYAJOzOAMmu6+KXxi8FfBTw7/bvjnxLp/hnSy2xJr6XDSvgnZGgy0jYBO1QTx0r4a/aa0v9o/8AaG0HQfsX7Lkfg/xh4e1K31LRvFEPjvS7meyaNwWQKBGSjAYK7wMhTg4r1f8Aac8VfCXwT8dPhp4o8cWfijxt8TtN0+U6F4C8MWS6kxL58y6+zbfvgg7WMg/1WVBKEhv4U9ne3fpe6X4W6Wvewur66X7dbWb/ABv12tc9O+En7bXwQ+OfiRfD/gv4gWOqa3ID5VhcW9xZSzYBJEa3EaeYQASQmSACa+fv2lf27vDvwt/bM+HXhW58ezaP4M0EXreM7OLT7hlS4e0JtFcpEXlXMiHEZZQSC3KjHm37Vvxc1n4o/FD9nnxJJ8GPEvw5W08d6fb23iPxStvaX0weQFrX7MrNJsIXduY7Rtxj5q9w/aA/5SP/ALMf/YO13/0lkq6cXKdN7azVvSHMn+O3ezvbdSdoVP8ACn97s1+G/qrH2JY3sOpWVvd2z+Zb3EayxvgjcrAEHB5HB7182ft//FjWfh78F7Tw74Qv7jT/AB3451a28N6JNZytHcQyTOPMlRlIZSqZAYEEF1NfTVfmx8cfj5BrX/BQ7Tbx/BXjT4g+FvhNYPCtp4J0c6k8erXKZLyjcqqqr8oJOd8PA64yfLKpGD2bu/8ACtX9/wAPTVouPNGEp9UtPV6L7nrbXRPc93/YN+I3iJofiJ8IPHet32veNfh5rctqdS1Wd5rq/wBPmZntp3dyWYkbhyThSlfRHxI+KHhP4Q+F7jxH4z1+y8OaLAdrXd9JtBYgkIg6u5wcKoJOOBX5xax+0xa+Hv29vAvxVh+HvxA+HnhvxVap4T8RSeNdBOmxTyscW8qOJGViu2LdnBCxHGcnHuHx50u0+Jv/AAUZ+C/g3xJCl74Z0bw7eeI7bT7gboLi+3yIpZDwxQRI464x6E1fvVI0m93dN+cU23bzik/WW5n7tN1LbKzX/bzSSv5SdvRGB+09+2h4M+Kvwl8N3nwb+Jc0l/D410i1vl0ua5067+zySMGV43EchibgHgqelfYPxV+Mngr4IeGW8QeOvElj4b0nd5azXjndK+M7I0UF5GwCdqAnAPFfLP8AwU3+G3h/UvCHw28YyWdvD4j0nxlpVrBeqgWWSCWXDwlupXIVwO2046mneKtJs/if/wAFSND0bxNBHf6T4P8AAra1o9jdDfELyS5VGnCngsAwwexiU9VGIp+97kd3OXna1OMvLotu7Kn7suZ9IR/Gcl+u/ZGR8fv2vvC3xZf4E3nwg+I811bXHxN0rTtXh0q4uLGaS3k8zMNxCwSQxPt6Ou1tvfFe2+JNS0+2/bT8ORTfFbU7C8HhKaUfDhLS6azvIxLLm/aVX8gOuCu1lL4QYOMV5H/wUE+HPh//AIWr+zd44Syt7fxKnxE0rSnu40CyXFu8vmbHI5YI0YK56b2x1NafjL/lK14C/wCyc3P/AKUz1rDWMbaPnn57Uk/67XdtdRzVoyb/AJYfjVt/Xor6XRyn7OP7e/hn4mfthfEfw9dePptR8M6s+n2HgWx/s64jilZYna5AHkgo2/OWmwSAADgCvd/2YbyxuvGnxpW0+Kmp/EaSLxZOk+m6ha3UKeHHy2bCEzOyui/3ogqccCvMv2YP+T+f2r/97Q//AElNeTfDfxXqfgf4cft7a7os72uq2PibVpba4j4aJ9soDj0K5z+FYuap0YzttS5vxh+Our/LW9yjzVZRvp7RL/yWX/A09fK31L49/b2+APwz8WS+GvEHxK0231mFzFNBawXF4sLg4KSSQRuiMCCCrMCO+K9VuPil4Tt/hzdePl120u/B1tYyalJrFixuoTbopZ5F8oMXwAeFBPGMZryH9h74VeFPCf7JHgG00/R7F4df0K21HVmeFXN/PcQq8pmJB8zliuGzhVA6DFfLXw/s4vAPgX9u/wCGmilk8GeHYbm60q1DZjtGubO4aWFPRVMaDHbHrmrrJ0XVpvWUIt36e60mrfPe5NG1Z05bRlJLz969n+G1uvkfVPin/goD+z74LbR11f4lWEEmrWkN9bRxWl1O4hmRZImlWOJjAWR1bbKFOCCRXuXhvxLpPjHQbHW9C1K11fSL6ITWt9ZSrLDMh6MrKcEV86/sGfC3wrpH7FvgWwi0OxktvEOireasssCt9uknBL+dkfOMNtGc4UAdBXKf8EqS0P7Md/p6sxtNO8U6paWsbHPlxCRWCj2yzH8a1lFRq1KX8qv+KVvxWvXsjCM3KnCr0k0vvTd/wenTuz7HooorI1CvgD/gnD/ydN+2h/2Oa/8Apdqtff8AXwB/wTh/5Om/bQ/7HNf/AEu1WgD7/ooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPhz9oL/gnpd2fjWT4tfs667/wrb4mQF55NPhITT9SY4LJtwViL45UqYnONyrkvVn9nn/gopBfeKh8Mfj5op+FfxPtWS38y+BjsNRkPAZWPEJbtljG3VX5C19tV5L+0R+y58PP2nvCraN430ZZ540K2esWoWO/sSe8MpBwM8lWBQ91NAHrVFfmdHqX7R3/AATTjEN/A3xr+AtpkRzxZW90iDJxuOC8IUAcHfDjADRluPtj9n79qT4cftNeHzqfgXX472eFA93pNxiK+s8nA82HJIGeAwyp7MaAPWaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAK4T49Ref8AA34ix43b/Dmorj1zayCu7rkPjFH53wj8bpjdu0O+XB75t3oA+af+CTMvmfsU+F1zny9Q1BenT/SXP9a+xa+L/wDgkXJv/Yy0cZzt1e/X6fvc/wBa+0KAKesWj6hpN7axlVkngeJS3QFlIGfbmvEP2H/gH4g/Zp/Z50fwH4nvNNv9Xs7q6nkm0mWSS3KyzM6gNJGjZwRn5evrXvdFEfdcmuqS+53CXvKKfR3+9WPnj9s/9njxH+0V4X8Cab4bvdLsp9B8VWeuXLarLJGrwRLIGVNkbkud4wCAOvIqf9pv9mLUPjBrvhLx14J8T/8ACE/FDwg8jaTrEkAnt5YpBiS3nj7o3Izzjc3BzX0BRSt26O/zsl+S/PuO93r2t8rt/qz5Lb4Q/tRfFjVdIs/iP8SfCfgbwrY3Ud1cp8Lft8OoakEOfJeecqYlPfYee4PGLnxy/Zn+I037QWk/Gv4O+I/D1j4uh0f+wr7SfGEM8lhdW28sG8yHMitkjgAZ2j5hyD9UUU+1tLNv71Z/hoLvfW+n43/PU+G/it+yL8fPjlrHgDxf4z8e+EZvEHhTX7PU7fwvo9vc2mixRRyb53851lnlmbZGF3KqqA396vSv2of2eviH46+LXwy+Kfwt1fw1aeLvBi3kC2Hi1Lj7DcRXEexiWgBcFQW4AGdwORjB+mqKNrculm382rP70G9763Vvldv9TLgbWv8AhGI2mjsW8RfYwXjjkcWhutnIDFSwj399pOO2eK8N/Yr/AGcNc/Z58B+If+Ey1Kw1rx74o1u41rW9S013eGSR2+RVZ0RiAMtyowztjjmvoaine0pSXVW+V76fNL7kK3uqL6O/4Nfq/vPFf2w/2el/ac+Auv8AgiGW2tdZk2Xek3l2WWO3vIzlGZlVmVSNyMQCdrnANcB47/ZX8d/EPwL8K/Eb+LdP8NfHvwFaiODxFZK93YXjFNksUyuiM0coAJO3Kl3wCDz9U0VKXLe2mqfzWl/u0fdaPQpvmtfomvk91/W258J/Fz9lT9pH9oyPwxdfEPxr4Csf+Ec1q01G08P+GYryKxn2SAyTzTTI0hlEe5UQLtyxOV7+zftGfs06/wCPvHnhf4o/DXxNbeD/AIo+G4ZLSC41C3M1hqdo5Ja1ulX5gmSxDKCRuOBnay/Q1FPoktLO/wA2kn+C+7TbQXVt63Vvkm3+b+/XfU+G/G37Kf7Qvxu+IHwx8ZfEbxr4JSbwf4lstSTw34bju4dOW2jlDzzCSVGkkuW2IqqwVAA3zDJr2bX/AIA+IdU/bY8M/GGK80xfDOmeE5tCmtXlkF407TSuGVBHsKYcclwc54r36iqT5Ukujb+clyv8AfvJp9Ul90uZfifLOm/s9/FP4c/teeLPiV4L1Xwje+CvHElgfENhrq3SahbJbxiM/ZDECjMRlgZCBk4xxuOp8Cf2W9Q8Eah8fYPGb6Vq+gfEjxFeajDaWUsjsLOcOpjm3Rrtfa/RSw96+kqKiy5OR6qzj8m07fginJuXP1un80mr/ifGXg/9n79pv4B+H/8AhA/hf8QfAuueAYGddLu/Gtldf2rpMLMSIo/IzHMEzkGTgnjaq4UdZ4O/Yyk+Hn7NvxP8FWXiEeJPH3j21vpdW8TasphW7vriJ0VmVQ5SJS3Qbjyx74r6hool78ZRlrzKzfW39ff1CL5ZRlHTld12v6f1boecfs6/DjU/hF8B/A3grWJ7W51XQ9JgsLmaxdngeRFwShZVYr9VB9q4n9i34BeIf2cvhTqvhnxLeaZfX91r97qqSaVLJJEIpipRSXjQ7htORjHua99oq3Jucqj3krP70/zRkopQjTWyaf3Jr8mwoooqSwr4A/4Jw/8AJ037aH/Y5r/6XarX3/XwB/wTh/5Om/bQ/wCxzX/0u1WgD7/ooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBGUMpBGQeCDXxj8fv+Cbfh/wAVeJP+FgfBvWZfhB8TbdjPDdaSzQ2FzJ38yNOYi3QtH8pBbdG5NfZ9FAH56eEf2/fiT+zb4gsvBf7Vngi60tGxFa+PNFgEtrd4/wCWkiRZR8j5j5WGXgGEZ4+6fAPxE8MfFLw1b+IPCGvaf4j0WfhL3Tp1lj3AAlGwflYZGVOCO4FW/FfhHRPHWgXmh+ItJs9b0e8Qxz2N9CssUikd1YY/HtXwn4+/4Jy+LPgr4kn8cfsr+OLzwXqzMHufCmpXTSWN2oOQiu+4EDoEmDjJzvSgD9A6K+BvAf8AwU6vPAHiS38F/tJ/D7Ufhf4k+4dYtoHl06fkDzAnzME5+9G0q+47fb/hDxpoPxA0C11zw1rNjr2j3K7ob7T7hZon46blJGeeR1HegDaooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAK5n4nRef8NvFkeN2/SbtceuYXrpqxPHEXn+C9fjxu36fcLj1zGwoA+QP+CQEvmfsdWq5z5eu3y9OnKH+tfbVfDX/AARzl8z9kORc58vxHer06fJCf619y0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFfAH/AATh/wCTpv20P+xzX/0u1Wvv+vgD/gnD/wAnTftof9jmv/pdqtAH3/RRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAc18Qvhr4V+LHhufQPGPh/T/EmjzctaahAsqhsYDLnlWHZlII7GvhzxZ/wTb8Z/BPxFP4v/Zd+JN94OvWfzJfC2s3DSWU4HOwSEMGHAASZH65MgxX6EUUAfn94S/4KXeI/g9r1p4P/ae+GmqeANYb5F8RaZAZ7GfGAZNilsrwctA8vPAUdvtn4e/FDwj8WNDTWPBviTTPEumsATcabcrMEJ6K4ByjcH5WAIweKveL/BegfEDQbnRPE2i2Gv6PcDEtjqVuk8L+hKsCMjseo7V8VfEb/glrpeia9L4u+APjvWvg/wCKuWW1t7uV7CTnOzIbzUUnqCZExxsxQB930V+dq/tiftJ/snmKz+P/AMK28Z+GIflbxr4TKn5AOZZAg8vJwflcW57/AF+n/gZ+2x8HP2hvKg8JeMbUaw+AdE1TNnfbj2WOTHmdRzGXHOM5oA9zooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACs/wARRef4f1OPG7fayrj1yhFaFQ3cXn2s0eN29GXHrkYoA+Fv+CM8vmfsl6muc+X4pvF6dP8AR7Y/1r7vr4F/4Ity+Z+yp4iXOfL8YXa9On+h2R/rX31QAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV8Af8E4f+Tpv20P+xzX/wBLtVr7/r4A/wCCcP8AydN+2h/2Oa/+l2q0Aff9FFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFADXVZFZWUMrDBVhkEelfMfx1/4Jx/A/46rdXVz4XTwrr8xL/2z4aItJNx6l4gDFJk4JLJuPOGGSa+nqKAPzub9n39sT9lkNL8LPiTZ/GDwrbDMfh3xQMXGwHIRRK/AAJH7udM44XoBteFf+Cq1l4P1lPDvx6+GPiT4Ua5naLn7NJcWsgBG59rKsgXkY2CUEc55Ffe9ZHinwhoXjjR5dJ8SaJp3iDSpSDJY6paR3MDkdCUcFT19KAOf+GXxu8A/GbT/tvgfxho/ieJV3yJp92jywjOP3kWd8Z5HDAHketdvXxR8UP+CT/wm8UamNc8B32s/CnxHGxkhu9BuWeBHIxuETtuXHpG6Dk1w7eHv25v2YMHStZ0n9oDwpbqo8jUBnUAg4JJZkmZzx/y0m7HH3qAP0Por4O8Df8ABWvwVbauvh/4weCPE3wj8RIB58d/ZyXEEfOMsNizrkg8eUcYPPHP2B8OPjF4G+L+mm/8FeLNH8T2yjLnTbxJXi9pEB3IeRwwB5oA7GiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPgD/gi5+7/Zr8ZwfdEfjO6+TuP9Dsx/T9K+/wCvgD/gjf8Aufgv8Sbbp5XjO4+X0/0a3HX/AID+lff9ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXwB/wTh/5Om/bQ/wCxzX/0u1Wvv+vgD/gnD/ydN+2h/wBjmv8A6XarQB9/0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAc743+Hfhb4l6O+leLPDul+JNNYEfZdUtI7hBnuA4ODwORyMD0r5D+I//BJj4U65qy678PdW174U+IYnMsFzot28sETkY3BHbev0SRAASMYxj7eooA/PJfB/7dX7NpU6J4k0T48+GbZQFtNVwL4pj5izOY5Wf/ttLzjg8itrwz/wVg8P+G9XTQPjX8NfFXwm10ABzcWr3FueQC+CiSheQRtR+O54J+86yfFHhHQvG+jy6T4j0XT9f0uXmSx1S1juYH6jlHBU9T270Acp8L/2gvht8aIBJ4I8baL4jfbua2s7tftCD1eE4kX/AIEor0GvjT4p/wDBKP4H+PLo6l4ctNT+HOtrIs0d14duyIlkByG8mTcq444j2YIB9c+fp8Bf21f2c/n+HvxU074xaHE3y6N4rOLlwCcKGnYlVxxhblevTgEAH6F0V+fNj/wVF8TfCm+TTfj98DPE3geXcE/tXS4jLbSse6rLsBUeqSydDxkYr6Z+E/7anwT+NQij8L/EPSJb6RVI07UJDZXWScbRFMFZiDx8uR05IIJAPbaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA+AP+CP/wC5+H/xcte8PjOf6/6pB/7LX3/XwB/wST/c6X8c7bp5XjOX5fT5SOv/AAH9K+/6ACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACvgD/gnD/ydN+2h/wBjmv8A6XarX3/X5k/se/GrwV8Cvj5+2r4i8c+IbPw/pq+MwIzcP+8uHF7qp8uKMfNI/wDsqCe/TmgD9NqK+ev2U/2voP2sLzxTd6J4F17QfCWlvEmn+INWCrHqZbcHVVH3WUryFZ+GG4qSAfoWgAooooAKKKKACiiigAooooAKKKKACiiigAooooATpXlvxZ/aM8LfBvUrKy19b4y3cRmjNrErrtDY5JYc5r0+dtsZr8+v+CgFw1x4q0QH+G0IH/fw1yYqrKjSc47nv5HgqWYY6OHrfC77eSPev+G8vhv/AHNX/wDAeP8A+OUv/DeHw4/556v/AOA0f/xyvzUj6irEfevC/tKv5H6kuDctf833/wDAP0k/4bu+HP8Azy1j/wABo/8A45Sr+3Z8OmOBDrJ+lrH/APHK/OJPvVdsv9cn1qf7Sr+Rp/qXltm7y+//AIB+x+karDrWm2t9b7vJuYlmTcMHawBGffBq7XEfCe6a48E6HnnFlCP/ACGtdvX1MdUmfh1SKjNxXRhRRRTMwooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCvfWFrqlnLa3ttDd2so2yQToHRx6FTwa+aviz/wTc+AHxcM89z4Ih8NanNk/2h4YkNg6kjk+UuYSc85aM8/U5+naKAPzz/4YC+PfwFjV/gL+0FfDT4OYvDvioE2ygDGFG2WIkjj/AFSdBz3D4f2yP2pfgKZIvjJ8ApPFOkW4w/iDwduIVQAfNk8szR4Pv5XX1GD+hNFAHyN8LP8AgqZ+z/8AEoRw3fiW58E6ixA+x+J7UwDOcH98heIDP95wfbrj6l8OeKNG8Y6TFqmgavY65pk3Md7ptylxC/APDoSDwR0PeuD+KX7MHwn+NUUy+NPAGh63PLndfNaiK8564uI9so/Bh2PYV8r+Jv8Agkr4c0C+l1j4OfE3xd8Ldc6oYLtp4MjoAUaOUdSMmRsZ6diAffFFfnxNa/t6/s/7Ps114X+OmhQkfLKqJeLHnkHPkSF+v8UuNw6gYFvSf+CsVj4L1CHSfjV8IPGPwy1RvlMn2YzQsw6ttlWJ9pGCNofqOo5oA+/KK8N8A/tnfBv4w6dIngv4leHpdYmjYWtlqs5spjLg7QYZgkjAHrtB4/Cvn34U/wDBQDxV8K/iO/ww/am0C38D67JIx07xbaoU0u8jLHaWOSoTsJVO0dHEZViQD70oqK1uob62iuLeWO4t5kEkc0TBkdSMhgRwQRzkVLQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAfAH/BKP9zqX7Q1r3h8ZyfX70o/9lr7/AK+AP+CWn7vx5+03B90R+M2+TuP3t0P6fpX3/QAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQB4F+2V8TPi/wDC/wCFlzqfwh8DReMNV2t9ouPN8yXT0A/1qWgG64PPAUkgjJVgDX4l/BGPxR8T/j5q2rXXgDTfit40vryfULjQtcvFsluLt5GkmcwCSIykMWJjHA5yuOn9GNfNP7TX7Afwy/aU8zVprNvCPjpf3lv4q0NBFceaOVadBhZ8EDlsPgYV1oA8M0v9or9s7Q9OttP079mHQNPsLaMRQWtrMIookAwFVVuAFAHYVa/4ae/bb/6Nt0f/AMC//umvbv2PPh/8e/hbb+IPDHxe8V6X420Cw8pPD2tRSvJfzJ8xcTMyhiANn3yzA5AZlANfSNAHwB/w09+23/0bbo//AIF//dNH/DT37bf/AEbbo/8A4F//AHTX3/RQB8Af8NPftt/9G26P/wCBf/3TR/w09+23/wBG26P/AOBf/wB019/0UAfAH/DT37bf/Rtuj/8AgX/900f8NPftt/8ARtuj/wDgX/8AdNff9FAHwB/w09+23/0bbo//AIF//dNH/DT37bf/AEbbo/8A4F//AHTX3/RQB8Af8NPftt/9G26P/wCBf/3TR/w09+23/wBG26P/AOBf/wB019/0UAfAH/DT37bf/Rtuj/8AgX/900f8NPftt/8ARtuj/wDgX/8AdNff9FAHwB/w09+23/0bbo//AIF//dNH/DT37bf/AEbbo/8A4F//AHTX3/RQB+fs37Tv7bLRkN+zdo4H/X3/APdNeH/GDx78VPH0yXXxW8D23gXVYcR2tpbSbxNFkkuf3j/xcda/W25/1TfSvz0/b2/5GvSP+vY/+hmvPx/8Bn13Cv8AyNafo/yPlaPqKsR96rx9RViPvXyR++xLCfeq7Zf65PrVJPvVdsv9cn1qDd/Cz33wl+0X+2BpOmQWug/s/wClappcKLHa3T3ODLEBhHP+kDquD0710H/DT37bf/Rtuj/+Bf8A9019f/B7/kSdF/68of8A0AV6BX30fhR/KVb+JL1Z8Af8NPftt/8ARtuj/wDgX/8AdNH/AA09+23/ANG26P8A+Bf/AN019/0VRkfAH/DT37bf/Rtuj/8AgX/900f8NPftt/8ARtuj/wDgX/8AdNff9FAHwB/w09+23/0bbo//AIF//dNH/DT37bf/AEbbo/8A4F//AHTX3/RQB8Af8NPftt/9G26P/wCBf/3TR/w09+23/wBG26P/AOBf/wB019/0UAfAH/DT37bf/Rtuj/8AgX/900f8NPftt/8ARtuj/wDgX/8AdNff9FAHwB/w09+23/0bbo//AIF//dNH/DT37bf/AEbbo/8A4F//AHTX3/RQB8Af8NPftt/9G26P/wCBf/3TR/w09+23/wBG26P/AOBf/wB019/0UAfAH/DT37bf/Rtuj/8AgX/900f8NPftt/8ARtuj/wDgX/8AdNff9FAHwB/w09+23/0bbo//AIF//dNH/DSX7cv/AEbl4f8A/Asf/Jlff9FAHwB/w0l+3L/0bl4f/wDAsf8AyZR/w0l+3L/0bl4f/wDAsf8AyZX3/RQB8Af8NJfty/8ARuXh/wD8Cx/8mUf8NJfty/8ARuXh/wD8Cx/8mV9/0UAfAH/DSX7cv/RuXh//AMCx/wDJlH/DSX7cv/RuXh//AMCx/wDJlff9FAHwB/w0l+3L/wBG5eH/APwLH/yZR/w0l+3L/wBG5eH/APwLH/yZX3/RQB8Af8NJfty/9G5eH/8AwLH/AMmVS1j48ftqeItNm0/Vf2ZPC2p2Ew2y2t5KksUg9GRrsg/iK/QyigD8X/iR+zL8X/iV5kkv7G3hjw5eOSRdeG9Sax259IkvPJ/OPjHpXyh8ZvAPxH+EtrbeE/GbXmk2MUnmQ+HrzxBb3pt3Axv+zxyHyjjK7igyMjPUV/Qz8afh7qHxW+F3iDwnpfinUPBd9qkCwx67pX/Hxa4dWJXDKfmClDgg4Y4I614f+z//AME3/g38B5E1I6M3jXxPu3trXiTbcMrdzHFjy0553YL8n5sUAfBP7B/xE/a9+HnhWG38D+Ab/wAZ/Ducq9vb+IoXjtoFLfM9nK8kZ2nnKqWTOTtySa/ZykVQqgAYA4AFLQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAfAH/AATH/c/Gj9rG26eV4z+76f6Tfjr/AMB/Svv+vgD/AIJr/u/2j/2xIPuiPxmPk7j/AEzUx/T9K+/6ACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAIrn/VN9K/PT9vb/AJGvSP8Ar2P/AKGa/Qu5/wBU30r89P29v+Rr0j/r2P8A6Ga8/H/wGfXcK/8AI1p+j/I+Vo+oqxH3qvH1FWI+9fJH77EsJ96rtl/rk+tUk+9V2y/1yfWoN38LP1c+D3/Ik6L/ANeUP/oAr0CvP/g9/wAiTov/AF5Q/wDoAr0Cvvo/Cj+Uq38SXqwoooqjIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPgD/gnZ+5/a0/bLiHyhvFqvtPU/wCm6mc/+PfrX3/XwB+wH+5/bR/bAiHyhvEKPtPU/wClXpz/AOPfrX3/AEAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUV4F+1Z+01dfAu18NeHfCmg/8ACX/E7xhcmy8PaEX2xswxvnnYEFYk3AnkZ9VAZl4yP4Q/tbX1qutXH7QPhrTNYZfNPhe18Gwy6Wr9RF9qdvtGzsWxupJ3Tl02v5/m/l+Y2rWXVn1hRXzj+zD+09rnxH8YeKvhf8S9CtPCnxa8KhZLy0sZGaz1K1bG27td3zbDuXKknG9eeSF+jqprRNap6rz/AK/4G5KerXVBRRRSGFFFFAEVz/qm+lfnp+3t/wAjXpH/AF7H/wBDNfoXc/6pvpX56ft7f8jXpH/Xsf8A0M15+P8A4DPruFf+RrT9H+R8rR9RViPvVePqKsR96+SP32JYT71XbL/XJ9apJ96rtl/rk+tQbv4Wfq58Hv8AkSdF/wCvKH/0AV6BXn/we/5EnRf+vKH/ANAFegV99H4UfylW/iS9WFFFFUZBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQB+f/AOwyfI/bu/a1g6b9Ujk5HP8Ax8Tn/wBmr9AK+AP2Mf3P/BQz9qmIfKGnifaep/ek5/8AHv1r7/oAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigD4g8eZ/wCHtHw4/tXb9k/4Qe5/snzc7ftG658zZ23bN2fb8K+368E/aq/Zkn+O1r4b8Q+F9ePg/wCJvhC5a+8Pa9s3xo5xvgmXB3RPtGeDjHRgWVvAfjfpn7Uvxm8KaZ4V1L4PQ6T4n0m7W70/4g+EfiDFp9rb3QVkE4tWUzNGVZgY2ySGIGDSi7U4w6pv7nJyuunVqztt5lSV5ud9Gl8mopW720vdX3fbXa8fbf8Ah7R8Nf7K3fav+EHuf7W8rGPJ3XPl7/8AgWzr/s19v18I/sl/Cv4tfCD9pLxBq3xj8J3Xjbxd4wt1hX4laPexTadZ28UQb7K8GyN4AWjUbtuGYIAvBY/d1aW5aUI3vv8AjKT/AAvb/gambfNUnK1tvwil+NgoooqCgooooAiuf9U30r89P29v+Rr0j/r2P/oZr9C7n/VN9K/PT9vb/ka9I/69j/6Ga8/H/wABn13Cv/I1p+j/ACPlaPqKsR96rx9RViPvXyR++xLCfeq7Zf65PrVJPvVdsv8AXJ9ag3fws/Vz4Pf8iTov/XlD/wCgCvQK8/8Ag9/yJOi/9eUP/oAr0Cvvo/Cj+Uq38SXqwoooqjIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPgD9kf8Ac/8ABSf9p+Hpuihkw3X78Z/L5v5V9/18Afsv/uf+Co37ScQ+UNpsD7T1PNqc/wDj3619/wBABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUjHaM0tNkGVNAHh3x1/acT4GatawX/AIbmv7G6i8yK+iugilgcMhGw4Iyp+jCvKv8Ah5B4fPTwxcf+Bo/+Ir0X9p34dj4geC7uyMQe5izNbMe0gBG3PowJU/XPavy71LTpNK1Ca2kVlKNxuGDivExlavQn7r0Z+k5BluWZnhr1Kf7yOj1fye/X80ff0n/BRjQZkI/4Ri4Gf+n0f/EV83/tF/Gux+NGpWd/aWbWBt4/KMTybyfmJznA9a8PXoKsLXmVMVVqx5JPQ+4wWRYDBVlXoQtJebf5ssR9RViPvVePqKsR964D6qJYT71XLRgsiknAzVNPvVZj+7UHSldWPsPwX+29p3hXQ7HT28M3FwbeBIi63aqG2qBnGz2rov8Ah4Ppn/Qo3P8A4HL/APEV8RR9BTq9D+0cQlv+B8n/AKnZRN3cHr/ef+Z9uL/wUF012CjwhdEnsL1f/iK+pPDGsT65oVhfXVk2nXNxCsslm772hJGdhOBkjvX5u/s2/D0+MPHFve3EW+w05lmbI4eTOUX8xk/T3r9IfD8Lx2ibuuK97A1K1aHtKr32PyvifC5dl+JWFwMdV8Tu36I168D+K37avw9+F/jKfwba2/iDx/43t0Ek/hnwPpT6newLxzIFIRDyPlZwwBBxyK9B+PHjqf4Y/BPx54ttQDd6Lol5fwbhkeZHCzJn23AV4f8A8E0/h3Y+E/2W/DviRlF34m8YmXXNZ1aX5ri7lklcrvc8nauB9Sx6sc+jG8nLoo2+bd7fk7/Jdbr4yTUVHu7/AHK13+Kt/wAA6j4V/tvfD/4l+OIPBN/p/ib4c+NblPMtPD/jvSW0y6u155iyzIxODhd244OAcGvoOvLvjt+zl4Q/aHsfD0Pidb23udA1OLVdO1DS5xBdQTJ2WTaSFPGQMcqpyCAa8y/aQ+PPju3+MHhH4IfCNNNg8c69ZSarf69rEZmt9G09Cy+cIx/rJGZWCg5GQoI+bKu97K3vN2/C9/Lre/a/kK2rd/dSv6a2t59Letj6eor4j8efEj47/sX3/h3xL8SfHem/GL4Y6lqMOm6xfLoMOj32imU4SZFgJSSMHru5JwPlzmtb9ov46fFvw9+154A+GXw1u9Ne38U+HJ5fK1e3VrS0mWV2a9cqvmvsijYCMOqszLmjflUdbtr5pczTv5ddtd7XDbmctLJP5N2uvn038r2PsaiviXWviH8df2V/jN8MdO+IfxE034s+CPHmsLoLy/8ACPw6TdaZdSYERjEJIdSWGS5PCkfKcGtf43fG74g+LP2p0+Bvgjx7ofwiW30SPV5PEWqadFqF3qErvhbe1gmZY2AGSerfK2OlG/Ly63bXzS5nv5a+fQNr82lkn8m7L8dPLqfYdcL4J+NPhb4ieO/GnhLQrqa71XwfLBb6sWgZIoppQ5Eas2N5ATJIG3kYJOceZfB7Tv2h/C/jnXfCfxB1rSvG/hOTTPP0r4hWdjb2F1Fdk7fJmsVcg45YFRt4GWO4hfm39hv4f/Euz/a4+Okl/wDFj+0YNF1y3TxJD/wjltF/wkcjQzCOTcGzabDztjyG6GnD3qnJfTlb+6SX69usWrq4pvlhzdbpfem/x/zvZ2P0ZooopDPj28/4KbeCk8T+I9E0z4X/ABU8Sy6BqU+lXl1ofh+C7txPE5RgGW56ErkZAOCOBXRfDT/goh8MviB4+03wXqml+LPh14k1Rgmn2XjbSPsP2xicKqMruoJIwNxXJwBkkCvFv2C/jR8Pvhn4g/aGsvGHjrw14UvLj4j6lNDb65q9vZySx78b1WV1JXIIyOMis7/gop8YPAXx+0n4a/Dz4YeI9K8bfEm78U2tzpk3hu4S++wIocPI00RZUHKkrnohYjC5ope97JPXm5L/APb1r/de/ogn/wAvOnLzf+S3t99vxP0aor4v/aB+L3xmh/bM8JfB/wCHPiKx0ex8Q+ETdzXWoadFdR6bMs83mXoUqHkcRwhFjLiMs4JFavxW+L3xV/Z78I+A/hvD4i074qfGzxxqs1lpWsahpiabZw26YZ7iaCE4xGjDgHnJPO3aUtYprq7Lzd+X9OulvR2bXK+V9Em/JOPNr8u2v3o+u6K+J/iVrn7SP7JfhY/EvxP8StJ+MfhHT5Yjr/h8+GodKuLW2eRUaS0lhbMjIWH+s4xkkenQftPftOeINN8XfCDwP8P/ABNofgpPiNDNeL4416BZ4LO3WNHjWKJ2CPLJvUAOcZKjq2Q97KOrva3na/5J67OztqLbWWite/kt/PqtN9UfXFFfMvw70P8AaV+G/wAUvD9h4k8XaT8afh5qscv9o65/ZVrol7o7hcxssUcm2ZGJA4DHg/dwN3CeIvjF8Uvjp+094/8AhT4H+KGh/Bi18Gi2RHuNHg1TVNZkljDu6RTuqCJcgZUZGVJzu4N2lHVu7+7fe3l69A2TctErfjtt/S6n2rRXiP7PL/HDSNY8U+HPi4uleINP094jonjTTEitW1WNhlxNaI58p1OBwFB5AzgMfbqfZrqLumFFFFIYUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAfAH7Ov7j/grF+0RD03aDBJhuv3dPP5fN/Kvv+vgD4Hfuf8AgsF8fIh8obwnbvtPU/u9JOf/AB79a+/6ACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAwPE+krf2brtycV+bv7XHwpbw34kbWrSDba3bFn2jhZOrj8fvf99V+n00YkQg14b8fPhpD4y8M31iyqryLujkIzsccqfz6+xIrkxVH21Nx69D3clzF5bjI1X8L0l6f8Dc/KtegqwtXfEmhzeHdaubGeNopIpGUo3VSCQR+BBFUlr5F7n9BU2pJNbFiPqKsR96rx9RViPvWZ2RLCfeqzH92qyfeqzH92s2dUSxH0FWLO1kvrqKCJGkkkYKqqMkknAAqvH0Fe7/ALLvw2bxN4mOs3MW61sWAiyOGlPf/gI5+pFbUKLr1FBHBmuYQyvBzxM+i0830Ppv9nb4Xp4O8L2du6L9pYebcOP4pD1/AcAewr6CgjEUYArI8N6WtjZooGOK26+5jFQiox2R/L9atPEVZVqjvKTuzn/iD4NtPiJ4D8ReFr8kWWtadcadMy9QksbISPcBq+M/2Nf2i9C/Z48Ir8BPjVq9r4C8Z+D5ZrezvNckFtY6pYGVmhnhuHxHjDbQCQSFGMkMF+7K5/xl8PPCvxEsUsvFfhnR/E9mh3Jb6zYRXcan1CyKQDTV4ttbPf5bP5Xfqn6WydpJJ9NV8916Oy+aR8qfH/8AbQm8Xa/4a+Gf7Nuvad4x+I2rX8Ml1qemImoadpVgrAyyzyjdGQeAcEkAnkMUzkfHDXI/2cf28PA3xZ8Zu8PgPxB4Vbwld+IBC3kWF6sxlQzbQdiv8uCfVj0UmvsHwb8O/Cnw5sZLHwn4Y0fwvZSNve30bT4rSNm9SsaqCa1dW0ew8Qabcadqljb6lp9yhjntLuJZYpVPVWRgQw9iKa9yzjum3r5x5beSt+OvkL4rqWzSWnk7383e3y08z4Q/b4+OHhD9oj4d6N8EvhZ4g0zx/wCMfGWrWahPD90l7DY20UqyyTzSRFlQDYuQTnG44wK6vx5aiw/4KcfBW2B3CHwPfxhj3wJh/SvqbwT8KfBPwzFwPCHg7QPCguceeNE0uCz83HTd5Sru/GtG68F+Hr3xTZ+JrjQtMn8SWcLW1rrEtnG15BE2d0aTFd6qcnKg4OTTjaDi13k384OC+7/MmpepFp9kl8pqT++1j5N/4KGf8jn+zF/2U3Tf/QhVD9qHXvgP8RPj8Phj+0B4NsfD8EWlJfeHvHep6kbKO8BP7yBZ02eXsYt8sjlSRnAJXP2B4i8F+HvF02lza7oOma1Npd0t7YSajZx3DWlwv3Zoi6ny3HZlwR60zxh4D8M/ELSxpvirw7pPiXTg28WesWMV3Du9dkikZ98VFvd5Xr7zl98Yx+TTV/wNObW600S+6Tf43sfAX7MMdp8M/wBsrSvh/wDBL4o6x8TPhG2hT3evWl1qS6nYaNJ8/kCCdAI1JfYNqc4J3Fu3c/sneNNA8M/tpftPeHdX1vT9K17WPEFk+m6be3SQ3F6BDKx8lGIMmFIJ2g4BBr7E8H+A/DPw80s6b4V8O6T4Z04tvNno9jFaQlj32RqBn3xVXUvhb4M1jxfZ+K7/AMI6FfeKbMAWuuXOmwyXsGM42TlS64yeh7mtIu0otu/uuL76yUvwskvIylG8ZJaXaa7aK343uzN8F/G7wV8QvHPi3wd4f1r7f4j8JyRw6zZfZZ4/srvu2De6BHztb7jN0ruawtF8B+GvDeuavrWk+HdJ0vWdYZX1LUbKyihuL1lztM0iqGkIycFicZNbtSvhV97a+vW3kW/idtunofnR+w1+z/8ADf4veJP2g9Q8a+CNE8UX1r8RdSt4LjVLNJnjj3ltqlhwMkn8a+2fh98Afhr8KLyS98G+A/Dvhm+kQxveaZpsUM7KeSpkVdxX2ziuj8M+B/DngttSbw94f0vQm1K5a9vjpllHbm6uG+9NLsUb3PdmyT61t0R92MYrokvuSX4ifvSk31bf3ts+NfGX/KVrwF/2Tm5/9KZ64v8A4KafDTQrz4gfBj4ieO9BuvEXwq0W8uNM8Uw2rTKbWC42eVcMYWEgRXBJKnkqq9WAP3JN4L8PXHiy38US6Dpkvia3tjZw609nGbyOAkkxLMV3hCSTtBxknita4t4ruCSCeJJoZFKPHIoZWU8EEHqKi1lT7xbflrKT/J2/E0cuac29pJLz0jGP5q5+aXjz4Zf8E8/BPhu01Sy0iw8bXt9NFBZaD4Q8TX+o6ncySMAqrAt4Cp5/jK9MfeIB9m/ae8RfB3wzb/Cf4YfFv4ZiD4WavZC2sfEOq3bougXEUQEVtJIhMkblQqmQTDgHJYKxH0p4V+Bvw48C602seG/h/wCFvD+rtkNf6VottbTnPXMiIG5+tdNr/h3SvFek3Gl63plnrGmXA2zWWoW6Twyj0ZHBUj6irlrG26ve3T/h1un36WveFvfra1+v/DdLfjtb8zNJ0Hwf8CP2j/hLo37L3xa1HxbaeINb2a/4LsdbTV9Kt9O+UzTsY8rGVXdguWfPIIxg+lfGy6/Zu+O3x68Z+B/jz4YsPh14s8PpF/ZXijUtY/s86vZuuVmSf93GdvACSF8ZOPusB9oeCfhT4J+Ga3A8H+DtA8KC4x5w0TS4LPzcdN3lKufxqTxt8MfB3xKt4Lfxf4T0PxVBAxaGLW9NhvFjJ6lRIrAH6UPVRT1tffztaz30t+L20sLRtrS9tvK+/TW/4L5/FX7DGo3vh/8AaX8f+BPAfxG1n4p/A/R9Fgkh1XVrsXsdjqDMm23guAArrs8wkRgLx0yMn7B+HHxv8FfFvWPFel+E9a/tW+8LX50zWIvss8P2W4BYFMyIoflG5QsOOvSul8M+FdF8F6PDpPh7R7DQtKh/1VjplqlvBHnrtRAFH4Cq/hvwH4Z8G3mq3egeHdJ0O61af7VqM+m2MVu95MSSZJmRQZHyzfM2TyfWrcrpJ62W/Vu99fK11321IUbXa0u/la1vvvZ9t9DdoooqCwooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA+APhL/o//AAWS+NfbzvBlv97v+50jp/3z/Ovv+vgD4e/6P/wWS+JvbzvBkP3u/wC50/p/3z/Ovv8AoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigArI1/TVvrR1IzxWvTZF3qQaAPzl/bD+E7afqSeILSA7ZW2T7R0cD5T/wIDH1UetfLS1+s3xk8BW3irw/fWU6ZiuIyhI6g9mHuDgj6V+XXjvwrc+DvE17pt0mySGVlPGB9R7EEEexFfNZhQ9nP2i2f5n7Nwnmf1rD/Vaj96nt5x6fdt9xjR9RViPvVePqKsR968c/RYlhPvVZj+7VZPvVZj6Vmzqia2gaTca7qlrYWsZknuJFjRR3JOK/SD4H/Dq38IeHLGyiQYhQbnxgux5Zj9TmvmT9kv4XtqWoHxFdRfKhMVqGHfo7/wDsv/fVfeGh6etnaooGOK+py3D+zp+0lu/yPw7jLNvrmKWEpv3Ke/nL/gf5mlGgjUAU+iivYPzsjuLiK0t5Z55EhgiUvJJIwVUUDJJJ6ADvWZ4U8YaD480ODWfDWt6d4i0ecsItQ0m7jureQqxVgskZKnBBBweCCKr/ABA/5EPxJ/2Dbn/0U1fE/wDwTT/aB+F3gP8AY/8ACGjeJfiT4R8O6xBcXxl0/VtdtbW4jDXcrKWjkkDDIIIyOQQaUHzSmn9lJ/e3/kEvdjFrq2vuVz7c8T+OPDnglbBvEXiDS9AXULlbKzOqXsdsLm4bO2GPew3ucHCjJOOlbdfnr/wUE+NXw9+Jg+BVh4Q8eeGfFd9B8RtMnltdE1i3vJY4/nXeyxOxC5IGTxkivqb9of8Aaa0b4BDQNLGjal4w8a+JJmt9D8LaMoa5vXUAsxJ4jjXI3Oc4z0ODgT927/msvPSL/UPtWXa/4v8AyPZKK+XfDv7ZXiTw9438PeG/jT8H9T+EI8SXIstH1g6zbavp81yfuwyzQhRC7dFBBz7AE12fx8/agtPg54m8OeC9E8Lap8QPiL4jSSXTPDWkvHETEmd0080h2wx5BG456HjAJDeln300117aderXbUO/lr207+h7fVa61Ozsrm0t7i7gguLtzHbxSyKrzMFLFUBOWIVWbA7AntXy54X/AG1PE+j/ABX8LeA/jD8GtT+FN94qmNtomoJrVvrFncTD/lm8sKqEYkqABuOWXIAOa8P/AGkPiN8UNJ/4KMfDSbRvhIdevNJ0rUYdBsf+Eltbca5A8Tebcb2XFtsyw2Pkts46inH3pwj0lfX0Tf37abpO+yYpaRk+qt+Lt92+vlbdn6OVw/jL46fDf4c6suleLPiD4V8L6o0SzrZazrVtaTGMkgOEkdW2kqwBxjg+ldpbySSW8TyxeTKygvHuDbGxyMjrj1r4P8eeBPDXxE/4KtWWk+K/DuleJ9K/4VwJvsOs2UV3B5i3ThX2SKV3DJwcZ5NTrzxgut/wTf6DuuRz9PxaX6n1Rpv7T3wc1i+hsrD4s+Br68mYJFb23iSzkkdj0CqJSSfpXpasGAIOQeQRXzz8YP2Xf2cNN+GviG48T/DrwN4X0WOzka41a10i1sJrcbT88c0aKysD0wck4HPSvP8A/gm3441DRP2G9M1/x1qElroejvfPaajqRIK6XCxKOSedq4kVf9lVA4ApxcWp305Un5Wen3/pfsElJclteZ289r/12du59j1n+IPEWleE9Fu9X1zU7PRtJs08y5v9QuEgghXpueRyFUc9Sa+UdP8A24PiH4z0h/F/gb9nDxP4o+GS7pI/EEmsWtne3UKk7pbfT2BklUgErtb5vY8V03xY+Pnw8+LH7EPiz4jxaM/jfwTcaU8l3oM15Jp80pWRVktpZI8tC6twSuenBIINZ1JOFKdT+VX16eq3t8ioJSnGHd20/R7fifR+m6lZ61p1rqGn3UF9YXUSz291bSCSKaNgCroykhlIIII4INWa+fNT/aQ8EfAX9mPwB4svNJvLKw1PTNOtdC8K6YzXt5NLLAhhs4S2DIwXje2M7cnkgHjLj9tvxr8O5NP1T4w/AbW/hp4GvriO2XxNHrdtqqWjSMAjXcMSq9umSASckE4wTXROKjVlTXR2179r7X8rmMJXpxm+qvp2723t8j62oryT9oL9pbwx+zz4R0rVtTgvtf1HXLpLHQ9D0SIT3eqXD42pEucYwQS2ccgDJKg+V6f+2x4p8G+LvDemfGj4K6r8J9H8SXi6fpev/wBt22rWn2h/uR3JiVTblu2cnrxhWIiPvS5Vve3z7evluaP3Y8z2tf5d/Tz2PqabUrS3vrezluoYry4DNDbvIBJKFxuKrnJAyM46ZFZ1j408Pan4m1Hw5Z69pl34h02NJb7SYLyN7u1RwCjSxBt6BgQQWAzkYr89/GXxJ+Klj/wVAgudP+EB1TUrXwrNptlpv/CT2sX2vS/tjY1PzGXbHn/n3Pz8da+ivhb4o8IX37cnxo0TTvBH9l+L7HSdLk1PxV/a0039pxtDGY4/srDy4dgIG5SS23J60qfv8j/mUvX3b/0/mt0x1FyOcf5eX095x/zsrX6PZ3PpiivlLUP22vEnjbxZr+k/BD4Nat8XdP8AD901jqevHWbfR7Dz1+9HbyzBvPK98Y7EZDKT6P8As7ftP6F+0HZ69aRaVqPhTxj4cmFtrvhfWUCXVhIc4ORw6NtbDjGccgUk0483S1/l39PMUvddn3t8+3r5Hs1FfFnw0/4KC+L/AI6eDhqHww+Aur+MtatJpYtXtf7egsbCwIkYJGLyeNRNKyBZDGkfyiRcnNe3/szftMaT+0l4b1m5g0bUPC/iPw/ftpeueH9UAM9hcr1XcOGU4IDYB+U5AxVWbv8Af8u/pqtRz/dy5Zd7fPXT10Z7JRRRSEFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAfAHhf/AEf/AILJeMO3neDI/vd/3Nr0/wC+f519/wBfAGn/AOj/APBZLUu3neDB97v+5j6f98/zr7/oAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAztYsVvLZlIzxXwt+2J8JS0f/CQ2kOJI8R3G0dv4HP0J2n6j0r75ZdykV518TfCNvr2k3UE8IlhmjaN0P8SkYIrCtSVam4M9PLcdPLsVDEQ6b+a6r+up+RsYKtgjBFTx966n4n+CLnwJ4uvdPnBISQ7HIxvU8q34j9c1y0fevi5RcZOL3R/SWHqwr041abumrosJ96ul8D+Gbrxd4hstMtF3SzyBc4yFHdj7AZP4VzUYLMAOSa+wv2Q/hYY7U6/dRfvrnKQZHSMHk/iR+QHrW+FofWKqj06nmZ5miyrAyrL4npH1f+W59K/CXwTb+GtDs7S3i2QwRqiDvx3PvXqCLtUCqWlWa2tuqgYwKv19mlZWR/N8pOcnKTu2FFFFMkwPiB/yIfiT/sG3P/opq+Fv+Cb/AOzB8JfiT+yN4S1/xT8O/Duv63cz3yzX+oWCSzSBbqVVBYjJwoAHsK+/NY0yLWtJvtOnZ0gu4Ht5GjIDBXUqSMg84PpXDfs//AvQf2b/AIW6X4C8NXeo32j6c80kU+rSRyXDGWVpG3NGiKeWOMKOMdaVNKMqjfVRt8m7/mOfvRgl0bb+aPiz9vT9n34a/CKT4Gan4K8D6H4X1C5+IumW01zpdmkLyRfO2wlRyMqpx7CrP7TXhvxlrX/BSrwBb+H/AIhL8Mb7UfBslvouuzaNBqivMsszTW6RTEIHZD97OcYH8VfX3x2/Z48OftCQ+EYvEV7qlkvhjXINfs/7LljjMlxEGCrJvjfKHccgbT7ipfjt+zr4G/aM8O2uk+NNMkuGsZvtOn6jZzNb3lhN/wA9IZV5U8Dg5U7RkHApK6s30k38nBR/zduuz3B2fMu8UvmpOX+Xputj5X+Pn7JvxO8ZeCbbTfi1+19pkPhk6hBLC2qeCtN01ftakmLZMtxGwf72AGyeeDXc/Gf40eJJP2oNP+Gnwf8AAng/WPirb+Hvt994w8YK0cNhYlwBCGhHnuGZlJVWwC44PzFej8I/sCeBdF8X6R4j8U+K/HnxVvtGlE+lxePvEDalBYyjGHjjCIuRgfe3DIBxkA10nxy/Y98F/HTxdpni+41XxN4M8a6fB9kg8S+DtUOn33kZJ8ovtZSuWb+HPJGcVWyiul23bzjZa97pX8lYW7b62svvu/lbbzdz48/amtPi9p/xm/ZoHxZ8b+E9RvLrx5YyWnhrwrpjwxQBZ4g8/nzMZXHzKu0gD5s9RXt/xm/5SY/AD/sXNX/9Fy10sn/BOv4Z3V5oGsXmseMNV8ZaPq1pq8fjDVdaN9qs72zM0ULyTo6iHLZKIiZIU54Fdz8fv2UPC37QeueG9fv9d8UeEPE/h4Spp+v+ENT+wXsUcgw8e8o42n2GeSM4JBqL5OTylJ/KUORfd5/LohSXOpLvFL5qXN/Vv8z2qvzv+N3wR8FfH7/gqFZeF/Hui/29oQ+Hq3YtftU9t+9S5kCtvhdG4DNxnHNfoRp1mdP0+1tTcTXZgiWI3FwwaWTaANzkAZY4yTgcmvNpP2ePDkn7RUXxnN7qn/CUR6H/AGALQSx/Yvs/mGTds8vfvyeu/GO1Tyr2kXulf/0mSX4tBd+zaWjdv/Sk3+CZ8OftafsA+Cf2d7LS/jJ8LfA1nreleF5BP4g8D61JNf2d9ZfxzKZmdwyA5IJK4G7HylW9j/ay8daX8aP+CaPibxL8NVRNCvNHtZo7S1RY/stvHcRefAUXhTGqOrKOAEPavsy6tYb61mtriJJ7eZDHJFIoZXUjBUg9QR2rx34B/sp+Ef2dNG8VaF4bvtYv/DHiC7ku5PD+syw3FlZlwVeOBRErBGUqpV2fIRe+Sc5RlOlOk3o9V69n5Pfy1WzNYyUKkKqWq38139V+Pqjwb4J/Bb4++KPg/wCCtV8KftZw23hu50e1fT7aD4c6ZIsEPlKFi3GTJKAbTnnKnPNcfrvwd074M/8ABPr9oWw074oab8VTqV1d6ld6lpNvDbw2105hE0JjhmkRGDLuKgrjdjaK9guP+Cb/AIAtJr628NeOPiV4G8MX0jS3PhPw14oe20qQt98GFkY4boRu6cDArnf2zLD4Wfs0/sO+MPhroVxpHhUXmlNFpGhNdr9rvpGmjDuqOxkmbJBZ+cDqQBSxkuelWa3lFpLd662v6peb8hYWHJUpR3UWtdlppe3z9EeIftEaXr95b/sLy6d4rXwNbNYRWtv4km0+O+isL6S0tfIZoJSEYnBA3Hjk9q9k+MX7Lnxm8S/DPX9L+I/7XlhH4Ju4BFqbap4B0yztxGWGN03nJs+bbhgwOcYNe36H8BvDXxW/ZY8EeAPiJoMeq2EegadHPaylkkgnjt0G9HUhkdTkZBB5I6EiuAsf+CcfgGa40+LxR42+JHxC8PafKktr4X8WeJnutKiZPuAQqiZCjgAsRjg5Ga7MRFOrVpvZzk+6s32/q6snaxzYeX7qlUW6jFdtvP5/J3fU8t+JGhWvw8/aY/YlttT1yLxD4Z03SrvSLbxA20W95d/YkjglHzsAZG8pl+ZuowTX1B+0/wDFD4ffCf4f2OqfETQB4p0241a1s7HSEsIL2ae8diIjFFMwUsvzNkHIAOK3/jB8CPBHx18C/wDCI+MNEiv9GjZJbZYWMMtnIgwkkDpgxso444wSCCCRXmHw/wD2E/BPg3xtpPirXPFHjj4m6ror+Zo//Cea82pRaY/9+CPYqhhgYLBsFQRggGo53NpT6Scr905cz+d7q/a3YvlUVeK15VG3mk0vl3+fc4PUzu/4KvaEcFf+LZScHt/pj1mfDuG6uf8AgoT+1FDZZF5J4W0tINvXzDaRhcfjivbPjd+yL4X+NnjzRPG7+JPF3gjxhpNqbGLWvB2qixuJbcsW8mQlHBTczHAAzuIJI4rpfCf7P/h7wf8AHDxl8U7O91SbxD4qs7Wyvre4lja1RLdFRDGojDBiEGdzsM5wBXOoc0VGWmlRf+BXs/x/A3crObjrfk/8lcL/APpLPD/+CVN5YP8Asb+HbC3KJqmm6hqFtqsHSWK5+1SNtkHUN5bR9e2KxvhrdW+tf8FRvi1d6AyyadYeCrWy1qWD7hv/ADYSisRwXEalfUbSOxr0Xx5+wb4E8VeNtV8WeHvEnjb4W63rD+Zq8vgHXW01NSfn5pk2upOSSdoXJZickk16R8D/ANnnwP8As8+GbnRfBeltZpeS/aL++upmnu76YjBkmlYks3XjgDJwBmtaknVk6rVnZq3m4uP/AIDq2uuyMeVRi4R1Td7+XNzffpb8fI+ff+CTdvHD+yarpGqPL4h1J5GA5Y+YFyfwAH4U79jEBf2rP2tQBgf8JHYn/wAhzV79+z38AvD37Nnw7TwZ4ZvNTvtLW8nvRNq0sck2+VtzDMcaLgHp8v4mj4Z/AHw98KfiB8RPGGk3mp3Gp+Ob2K/1KK9ljaGKSNWVRCFjUquHOdzMenNVf95zdOTl+f7v/wCRZVT3lK3Wo5fK8/8ANHpdFFFQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQB8AXH+j/APBZK2z/AMt/Bhxnj/li3T1+6a+/6+APEH7n/gsl4Zxz5vgx85/643HT8hX3/QAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVT1G1W6t2UjORVykIyKAPir9rz4TjVNHfWreL/SrEZcqOWizk/wDfJ+b6bq+JthjkZWGGXgiv168eeHY9V0+ZHjV1ZSGVhkEEdK/Mn4z/AA5m8B+NrmzSM/ZZW327eqEnH4jlT9M96+ezKhZqtH5n65wbmnNF4Cq9VrH06r5b/wDDFP4T+Bp/Hni+z09FbyS26Vx/DGPvH+g9yK/Tj4ceFYNF0u3hhiWKKNFREUcKoGAK+d/2S/hOdF0NNUuYsXd+FcbhykfVR+Ocn6j0r690+1FtAqgdBXfgaHsaV3uz5XijNP7QxrpwfuU9F69X+hZUbRiloor0j40KKKKACiiigAooooAKKKKACiiigAooooAKKKKACuZ8R/DHwd4x1zTda1/wnoeuaxphzY6hqWmw3Fxac7v3UjqWTnn5SOa6aijqmHkFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAfAHjz/R/+CyXw57ed4Ml+93/c3/T/AL5/nX3/AF8AfFP9z/wWS+DuOfN8GT5z/wBcdV6fkK+/6ACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCveW4uIWUjORXg3xZ+Bdl8QNQ0yS5UobO5E2VH30/ijPs2B+VfQNQSWqSNkiplFTXLJaG1GtUw81VpO0l1Ob8H+Hk0q1RQgXAwABXVDimxxiMYAp9UYhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHwB8bP3X/BYn4DSD7zeELhDnpjytX/AMTX3/XwB+0F+6/4K2fs9SD7zeHbhDnpjZqP+Jr7/oAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACuD+O/gzWPiD8HvFugeHda1Dw94gvNPkGm6lpl5JaTwXKjdERLGQyguqhsHlSR3rvKKipHni43tcuEuSSkuh86/sC/Ga9+Nn7M3hvUNbuJrjxTo7SaHrTXUhef7VbnaWlJ5Lshjck85c1x/7Y3jPxJ4t+M3wZ+CXgvX9V8Pajr+pHW9ev9EvJLW4g0m3B3qZI2DKsh8wDnBMYFZnwht/+Gef2+PiL4Eb/RvDHxOsR4u0ZT8sa30ZIvIl/wBpsvIR2VVo/ZLVvjP8evjT+0BOn2nTzcnwl4VZuR9htP8AXSJ/syyBW+u8Vo6iqThXe1ud+sXZr/wZ/wCS31M+X2cZ0o9+WPpLVP1ULv1R7N8YP2xvgz8AdXj0fxz48sdH1ZlDGwjimvLiNSMgyRwI7ICOQXAz2ru/hn8WPB/xk8MReIfBPiGx8SaPI2z7TYybtj4BKOpwyOAQSrAEZHFfK/8AwS48P6fr3wY1z4najBDf+OfF2v6hPq2rTIGuCFmKrDuPIQY3BenzfSoPAeh2Pwl/4Kf+JvD3hSCPTdC8XeCV1zVtMtVCQLepclFmCDhSRu9MmRj3pxi04wnvJX06Pl5reeiav36WCWnM4bRdvX3uW/lrrbt1Os/4Jy+NPEPjj4W+PLvxHrup+ILq28b6paQT6peSXLxQp5eyJWdiVRcnCjgZNfV9fG//AAS9/wCSQ/ET/sf9X/8AaVfZFRH+FSf9yH/pEQ+3U/xT/wDSmFFFFMYUUUUAFFFFABRRRQAUUUUAFFFFABRRRQB8AftNf6P/AMFTv2b5j919KnjGeBn/AEwdf+BCvv8Ar4A/ax/df8FMP2ZJB95raZDnpjdN/ia+/wCgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPm39tP9mvxT8eND8K6t8O9Y03w58Q/DN7LLp+qam8iRC3nhaK4iLRo7DIKEfKeU7Zr0/9n34Q2fwH+C/hHwHZGORdGsUgnmjXCzzn5ppf+BSM7c+teh0UR9yMoraTu/kEvecZPorfqfH9r+zL8Z/2ffFnia5/Z/8AFXg9vCHiO/k1Ofwn48trnyNNuZMeY9tLbfOVbA+RsAADr1ruP2cf2YNY+HHj7xT8UPiJ4pi8afFHxNEltcXlpbGCy0+1XaRa2yE52ZVcscE7F4B3FvoiiiHuJW6Ky8ltb7tPTTYJe+231d35ve/36+uu54F+xr8AfEP7PHgXxXoviO80y9utW8UX2tQPpcskiLDNs2KxeNCHG05ABHTk177RRQtIxj0SS+SSS/BB1b7tv73dhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQB8Aftjfuv8Agor+yzJ13PKmP+2pGf1r7/r5p/a+/Y7k/aQvfC/ibw94tvPBPj7wxJnStYhy0cCs4ZzsXDF/lGGDDHPBrxb/AIYc/ag/6O01j/vxcf8Ax6gD7/or4A/4Yc/ag/6O01j/AL8XH/x6j/hhz9qD/o7TWP8Avxcf/HqAPv8Aor4A/wCGHP2oP+jtNY/78XH/AMeo/wCGHP2oP+jtNY/78XH/AMeoA+/6K+AP+GHP2oP+jtNY/wC/Fx/8eo/4Yc/ag/6O01j/AL8XH/x6gD7/AKK+AP8Ahhz9qD/o7TWP+/Fx/wDHqP8Ahhz9qD/o7TWP+/Fx/wDHqAPv+ivgD/hhz9qD/o7TWP8Avxcf/HqP+GHP2oP+jtNY/wC/Fx/8eoA+/wCivgD/AIYc/ag/6O01j/vxcf8Ax6j/AIYc/ag/6O01j/vxcf8Ax6gD7/or4A/4Yc/ag/6O01j/AL8XH/x6j/hhz9qD/o7TWP8Avxcf/HqAPv8Aor4A/wCGHP2oP+jtNY/78XH/AMeo/wCGHP2oP+jtNY/78XH/AMeoA+/6K+AP+GHP2oP+jtNY/wC/Fx/8eo/4Yc/ag/6O01j/AL8XH/x6gD7/AKK+AP8Ahhz9qD/o7TWP+/Fx/wDHqP8Ahhz9qD/o7TWP+/Fx/wDHqAPv+ivgD/hhz9qD/o7TWP8Avxcf/HqP+GHP2oP+jtNY/wC/Fx/8eoA+/wCivgD/AIYc/ag/6O01j/vxcf8Ax6j/AIYc/ag/6O01j/vxcf8Ax6gD7/or4A/4Yc/ag/6O01j/AL8XH/x6j/hhz9qD/o7TWP8Avxcf/HqAPv8Aor4A/wCGHP2oP+jtNY/78XH/AMeo/wCGHP2oP+jtNY/78XH/AMeoA+/6K+AP+GHP2oP+jtNY/wC/Fx/8eo/4Yc/ag/6O01j/AL8XH/x6gD7/AKK+AP8Ahhz9qD/o7TWP+/Fx/wDHqP8Ahhz9qD/o7TWP+/Fx/wDHqAPv+ivgD/hhz9qD/o7TWP8Avxcf/HqP+GHP2oP+jtNY/wC/Fx/8eoA+/wCivgD/AIYc/ag/6O01j/vxcf8Ax6j/AIYc/ag/6O01j/vxcf8Ax6gD7/or4A/4Yc/ag/6O01j/AL8XH/x6j/hhz9qD/o7TWP8Avxcf/HqAPv8Aor4A/wCGHP2oP+jtNY/78XH/AMeo/wCGHP2oP+jtNY/78XH/AMeoA+/6K+AP+GHP2oP+jtNY/wC/Fx/8eo/4Yc/ag/6O01j/AL8XH/x6gD7/AKK+AP8Ahhz9qD/o7TWP+/Fx/wDHqP8Ahhz9qD/o7TWP+/Fx/wDHqAPv+ivgD/hhz9qD/o7TWP8Avxcf/HqP+GHP2oP+jtNY/wC/Fx/8eoA+/wCivgD/AIYc/ag/6O01j/vxcf8Ax6j/AIYc/ag/6O01j/vxcf8Ax6gD7/or4A/4Yc/ag/6O01j/AL8XH/x6j/hhz9qD/o7TWP8Avxcf/HqAPv8Aor4A/wCGHP2oP+jtNY/78XH/AMeo/wCGHP2oP+jtNY/78XH/AMeoA+/6K+AP+GHP2oP+jtNY/wC/Fx/8eo/4Yc/ag/6O01j/AL8XH/x6gD7/AKK+AP8Ahhz9qD/o7TWP+/Fx/wDHqP8Ahhz9qD/o7TWP+/Fx/wDHqAPv+ivgD/hhz9qD/o7TWP8Avxcf/HqP+GHP2oP+jtNY/wC/Fx/8eoA+/wCivgD/AIYc/ag/6O01j/vxcf8Ax6j/AIYc/ag/6O01j/vxcf8Ax6gD7/or4A/4Yc/ag/6O01j/AL8XH/x6j/hhz9qD/o7TWP8Avxcf/HqAPv8Aor4A/wCGHP2oP+jtNY/78XH/AMeo/wCGHP2oP+jtNY/78XH/AMeoA+/6K+AP+GHP2oP+jtNY/wC/Fx/8eo/4Yc/ag/6O01j/AL8XH/x6gD7/AKK+AP8Ahhz9qD/o7TWP+/Fx/wDHqP8Ahhz9qD/o7TWP+/Fx/wDHqAPv+ivgD/hhz9qD/o7TWP8Avxcf/HqP+GHP2oP+jtNY/wC/Fx/8eoA+/wCivgD/AIYc/ag/6O01j/vxcf8Ax6j/AIYc/ag/6O01j/vxcf8Ax6gD7/or4A/4Yc/ag/6O01j/AL8XH/x6j/hhz9qD/o7TWP8Avxcf/HqAPv8Aor4A/wCGHP2oP+jtNY/78XH/AMeo/wCGHP2oP+jtNY/78XH/AMeoA+/6K+AP+GHP2oP+jtNY/wC/Fx/8eo/4Yc/ag/6O01j/AL8XH/x6gD7/AKK+AP8Ahhz9qD/o7TWP+/Fx/wDHqP8Ahhz9qD/o7TWP+/Fx/wDHqAPv+ivgD/hhz9qD/o7TWP8Avxcf/HqP+GHP2oP+jtNY/wC/Fx/8eoA+/wCivgD/AIYc/ag/6O01j/vxcf8Ax6j/AIYc/ag/6O01j/vxcf8Ax6gD7/or4A/4Yc/ag/6O01j/AL8XH/x6j/hhz9qD/o7TWP8Avxcf/HqAPv8Aor4A/wCGHP2oP+jtNY/78XH/AMeo/wCGHP2oP+jtNY/78XH/AMeoA+/6K+AP+GHP2oP+jtNY/wC/Fx/8eo/4Yc/ag/6O01j/AL8XH/x6gD7/AKK+AP8Ahhz9qD/o7TWP+/Fx/wDHqP8Ahhz9qD/o7TWP+/Fx/wDHqAPv+ivgD/hhz9qD/o7TWP8Avxcf/HqP+GHP2oP+jtNY/wC/Fx/8eoA+/wCivgD/AIYc/ag/6O01j/vxcf8Ax6j/AIYc/ag/6O01j/vxcf8Ax6gD7/or4A/4Yc/ag/6O01j/AL8XH/x6j/hhz9qD/o7TWP8Avxcf/HqAPv8Aor4A/wCGHP2oP+jtNY/78XH/AMeo/wCGHP2oP+jtNY/78XH/AMeoA+/6/POX9sn47/sh+MX0v9pDwhH4n8EXl0wtPHPhW2VUhUthQyLhCo4wjiOXGTmTirv/AAw5+1B/0dprH/fi4/8Aj1eC/tT+CfiH+z/4Xu7D4i/thXuq3F/bMF8KJZTXdxfIRja0JlKqh/vSYU4PU8UAfqP8K/jF4L+N3heHxD4H8R2PiLSpACZLV/niJ/hljOHibj7rgH2rsq/FD/gn/wDsU/H/AFfxVpnj7RNe1D4QeHWVZRrEozNqEWchFs2OJUPX98AhGCN3Sv2qtY5IbaKOWZriVECtMygFyByxA4GevHFAEtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV8rfBH/gnL8MPhJ4yvfGOsPqHxH8Y3F09ymseK3W4aElshlQAKZAMfvGBORldvSvqmigAooooAKKKKAP/9k=")}, coordinateSystem(initialScale = 0.1)));
end LenoirCycleIdeal00;
——————————————————————————-
モデル情報
シミュレーション実行
- LenoirCycle.WoutCycle
- LenoirCycle.fluidState[2].T
- LenoirCycle.fluidState[2].p
- LenoirCycle.effThermal
- p-V diagram, h-s diagram
Input
Variables
熱サイクルは成立し、仕事を生成出来ている。しかし、生成仕事は小さく、投入した熱量の1/10程度。意図通り、投入熱量の増大に呼応して、生成仕事が増大しているのも確認出来る。

加熱後状態(状態2)の流体温度。100 [degC] を超えているが、加熱に伴って圧力が激増しているため相変化は起きずに投入熱量に呼応して上昇している。

液体も気体同様に、加熱すると膨張する。そして、加熱を等容で行っている為、体積が増えられない代わりに圧力が上昇する(*ただしこれは圧縮性の再現を含む物性モデルを使わないと計算出来ない筈)。そして、それを膨張させることで体積・比エンタルピに変化が生じて仕事に変換され、熱サイクルが成り立つ。
記事の結論が、液体の水だけで熱サイクルが成立する、なのだが、飽くまで「理論上は」の話。サイクル計算上成立させられても、これを現実の機器で実装させられるかは別の話となる。容器、バルブ、配管、熱交換器等がこのレベルの圧力や圧力変動に耐えられるかが問題となる。後述の熱効率が低いことも理由だが、実装の困難さも液相の水だけを用いた熱機関が実世界に存在しない理由ではないかと思う。

上述した通り、投入した熱量に対して生成出来ている熱量は非常に少なく、熱効率が非常に低い。原因は大きく2点有る。1つはルノアールサイクルが、圧縮プロセスを持たない故の特性として熱効率が低いということ。2点目が、作動流体に液体を用いているため、膨張プロセスの圧力変化が小さいということ。

y軸レンジが0から1だと見え難いが、拡大すると、投入熱量の増加に応じて熱効率が上昇しているのが確認出来る。この点は気体を用いた一般的な熱サイクルで燃焼温度を上げるほど熱効率が高くなるのと同様だ。

p-Vとh-sの軌跡を観ると、確かに上述した図と似たものとなっていることを確認できる(p-Vの形が大きく違って見えるのは、物性から決まる断熱膨張プロセスの線(等エントロピ線)の形の差異)。


最後に作動流体を空気にした場合と水にした場合を並べて観ておこう。上述した、作動流体が水であるが故に熱効率が低い点が理解出来る。
作動流体を空気にした場合との比較(上:空気、下:水):
一瞥すると、水を用いている場合の方が仕事が多く取り出せるように見える(p-V線図に囲まれた領域がサイクルから取り出される仕事)かもしれないが、横軸方向の変化範囲に注目して頂きたい。空気の場合は膨張により体積が2倍以上に増加するのに対して、水の場合は数%程度しか増加しない。このため、投入した熱の殆どは等圧排熱プロセスで系の外に捨てられてしまい、有効な仕事として取り出される量は極めて少ない。(*軸レンジを揃えたグラフを並べたい所だが、範囲が違い過ぎて水のサイクルの図が潰れたものになってしまう。)


h-s線図も確認。この図では、線で囲われた領域ではなく、膨張プロセスでの縦軸方向の降下量が、作動流体1 [kg] あたりの生成仕事なので、熱効率の善し悪しを比べ易い。(今回はy軸レンジを揃えており、投入熱量も揃えている。)
下図の通り、水は空気に比べて膨張プロセスの比エンタルピ落差が小さい。作動流体の物性、というより液体か気体かで生じる違いであり、ほぼ総ての熱機関で気体が使われているのはこの為だ。


後書き・まとめ
冒頭で述べた結論の繰り返しとなるが。
- 液相の流体だけを用いても熱サイクルを通じて仕事を取出す(動力を発生させる)事は出来る。最もシンプルな理想熱サイクルの計算で確認した。
- 液相流体でも可とは言っても、熱授受に応じて圧力・密度(体積)に変化が起きるという特性が必要条件。完全非圧縮性流体のパッケージを使うと計算自体回らない。




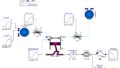

コメント