例題の目的・習得事項
本例題が目的としていることは大きく下記の2つ。
- 振子機構作成を通して、3次元剛体シミュレーション用のライブラリであるMultibody library内の一部のコンポーネントの使い方を学ぶ.
- PID制御システムモデル作成を通して、Blocks library内の一部のコンポーネントの使い方を学ぶ.
手書きスケッチと作成対象物の整理
作ろうとしているものを手書きで書き下す.熱流体の連載でもルーチン化している作業.
毎度酷い絵を描いているが、モデル化したい概念、機能が端的示す事が目的.それが可視化出来ているはずなので気にしてはならない.
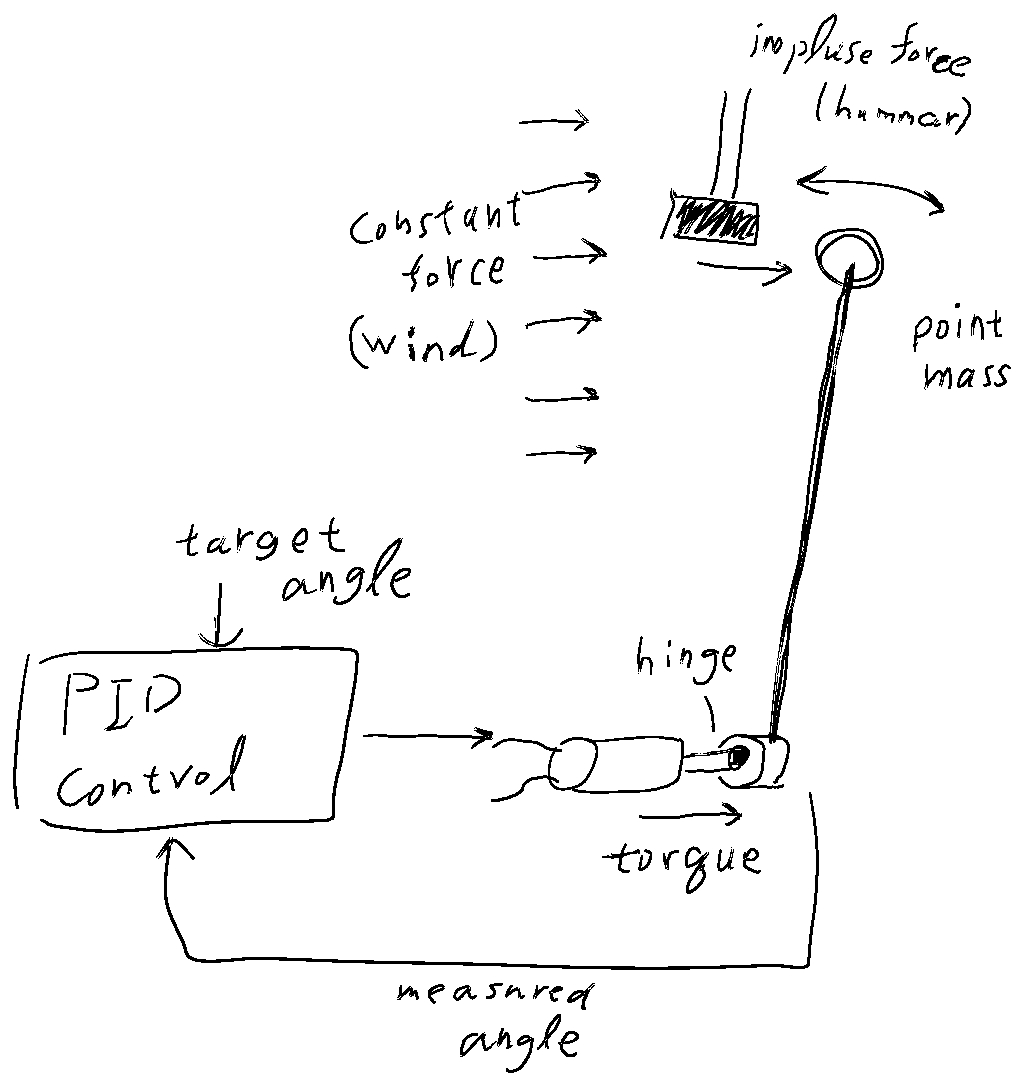
同じく定型作業として、モデル化対象物についての情報を纏める。極力簡潔に、箇条書きを並べるのがお勧め。
- 重力.振子を下端位置へと引く力.
- トルク入力.振子への入力は、振子根元ヒンジ部に加えるトルクとする.
- PID制御システム.
- 指令信号:振子の目標角度
- 計測値信号:振子の位相
- 定常的な外乱.常時、変化しない外乱力を加え続ける.横から風が吹き続けているようなもの.
- 突発的な外乱.任意のごく短時間だけ外乱力を加える.ハンマーで叩くようなもの.
- world frameとの接続.
- 制御システムへの指令(目標角度).
- 振子への定常外乱力.
- 振子への突発外乱力.
- 振子の角度.
- アクチュエータのトルク.
内包する物理現象:
今回は、例題の図によく見られる、根本が台車になった造りにはしない.
境界条件(Input):
これを通して重力加速度が振子に与えられる.
Output(注目する出力):
model(とpackage)ファイルの作成
熱流体の連載記事でも述べたように、必須ではないが、演習例題用のpackageは作成しておこう。過去記事の例で既に作成済みなら、そのpackageにmodelを作成すればOK。
コンポーネントの配置
下図の通りにコンポーネントを配置、接続する。
インスタンス名はコンポーネントを配置する際に自動で命名される(標準設定では名前を尋ねるウィンドウが出てくる)が、筆者は適宜、名前をつけた方が後々判りやすいものだけ命名している。下図のものだと解りにくければ、解りやすいように名前を変えてくれて構わない。
なお,テキストボックスやコンポーネント以外の観易さのための図形は必須ではない.
振子は、根本に当たる回転軸と、質点から成る.円柱/角柱型の剛体ではなく、根本の回転軸と剛的に接続された質点を振子とみなす.回転軸(ヒンジ)コンポーネントには3次元multibody用の他に1次元回転用のconnectorが備えられおり、回転ダンパ(後述の通り、ダンパの減衰は0に設定してしまうので繋ぎ方の例でしかないが)、軸の相差センサ.トルク入力境界コンポーネントを接続する.
直上で述べた通り、軸にトルク入力境界条件コンポーネントを繋ぎ、振子を能動的に操作するアクチュエータはトルクを自由に制御できるモータであるとする.
トルク入力コンポーネントの手前には、目標角度入力信号と実角度計測信号からトルク値を決定するための制御システムを置いている.制御則は同じみのPID.
振子の自由端、質点側には力を境界条件として入力するコンポーネントを2つ配置する.1つは定常的外乱力で、風が常に横から吹き付けているような力を与える.もう一方は突発外乱力で、台形波入力コンポーネントを使い、非常に大きな力を非常に短い期間だけ与える.ハンマーで叩くような入力を与えるようなもの.
diagramを見ると目に付くと思うが、ヒンジ、力境界、そしてそれに繋がる力センサコンポーネントは、余分な結線が伸び、”world”に接続されている.これはmultibodyの利用と、3次元剛体運動力学全般において難しさをもたらす部分.3次元剛体運動力学ではframeという概念、角速度、力、位置といったベクトルが”何に対してのもの”かの概念が登場する.これはそれらベクトル量の基準なるframeを定義するもの.
回転軸(ヒンジ)については、その接続は”a”の側は動かない外界に固定されているという事を意味する.力境界と力センサについては、その力入力のベクトルは振子先端質点を基準にしたものではなく外界を基準に指定したベクトルであるという事を意味する.

- Modelica.Mechanics.MultiBody.World
- Modelica.Mechanics.MultiBody.Joints.Revolute
- Modelica.Mechanics.MultiBody.Parts.BodyShape
- Modelica.Mechanics.Rotational.Components.Damper
- Modelica.Mechanics.Rotational.Sensors.RelAngleSensor
- Modelica.Mechanics.Rotational.Sources.Torque
- Modelica.Mechanics.MultiBody.Forces.WorldForce
- Modelica.Mechanics.MultiBody.Sensors.CutForce
- Modelica.Blocks.Math.Gain
- Modelica.Blocks.Continuous.Integrator
- Modelica.Blocks.Continuous.Der
- Modelica.Blocks.Math.Sum
- Modelica.Blocks.Math.Feedback
- Modelica.Blocks.Math.UnitConversions.From_deg
- Modelica.Blocks.Sources.Ramp
- Modelica.Blocks.Sources.Trapezoid
- Modelica.Blocks.Sources.Constant
使用コンポーネントリスト
必要なコンポーネントを見つけるのは慣れていないと意外と苦労する作業なので、総てのコンポーネントをリストアップしておく。今回特別取り上げておきたいもの以外、説明は省略する。
multibody libraryを使う際、基準となる絶対座標系(frame)を定義するためのコンポーネント.
multibodyでは複数の物体を配置したり接続したりすることになり、connectorからの相対的位置を入力するようになっている.そこで絶対座標系から位置をしていする際に基準として使う.
また、均一重力のような系全体に掛かる加速度を与える役割も果たす.
3次元空間用のヒンジ.frange_aと_bの間に1軸に関して自由に動く回転軸を成す.軸の向きは、”frange_aから相対的に軸のベクトルがどこを向いているか”をparameterで与える.
本例題では、frange_aを絶対座標(world)に接続し、_bに振子を接続する.
自由に運動できる単純剛体.
質量、質量中心(frange_aからの相対位置)、flange_aからflange_bへの相対位置ベクトル、慣性モーメント、慣性積を設定できる.
結果animationでは、デフォルトでは円柱と球体が表示されるようになっている.
multibody libraryにて、力を境界条件として与えるコンポーネント.
力をベクトルで与えるが、それをworld基準のベクトルとするか、接続相手のfrange_bを基準とするかを選ぶ.
力センサ.
読み値はベクトル量で、力境界条件コンポーネント同様に、読み値ベクトルを相対で定義するか絶対で定義するかを選ぶ.
parameterの設定
各コンポーネントのparameter設定を示す。コンポーネントを右クリックしてparametersを選択するか、ダブルクリックするとparametersウィンドウが現れるので、必要箇所に値を設定する。
下記リスト中で ” :: ” 表記をしているものは,タブやタブ内のグループによる階層構造を示す.表記が無いものは「general」タブ内のものだ.
尚、デフォルト設定のままにしておいて済むコンポーネント、parameterは記載を省略する。また、parameterの意味も特別説明が必要な者でないものを除き省略する.
- bodyShape
- General::r[3] := {0.6, 0, 0} [m]
- General::r_CM[3] := bodyShape.r [m]
- General::m := 1 [kg]
- Animation::length := bodyShape.r[1] [m]
- Animation::width := 1/8*bodyShape.sphereDiameter [m]
- Animation::sphereDiameter := 4^(1/3)*0.06 [m]
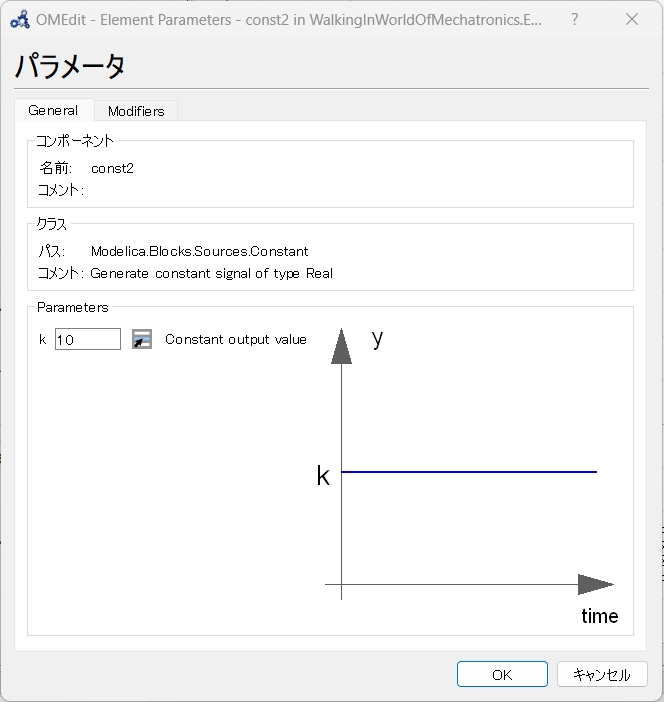
- const2
- General::k := 10
- constGeneral::(ゼロ信号用のもの複数)
- k := 0
- ctrl_D
- General::k := 1
- ctrl_I
- General::k := 40
- ctrl_P
- General::k := 30
- cutForce
- General::animation := false
- General::positiveSign := true
- General::resolveInFrame := resolveInFrame = Modelica.Mechanics.MultiBody.Types.ResolveInFrameA.frame_resolve
- cutForce1
- General::animation := false
- General::positiveSign := true
- General::resolveInFrame := resolveInFrame = Modelica.Mechanics.MultiBody.Types.ResolveInFrameA.frame_resolve
- cutForce_body_b_tot
- General::animation := false
- General::positiveSign := true
- General::resolveInFrame := resolveInFrame = Modelica.Mechanics.MultiBody.Types.ResolveInFrameA.frame_resolve
- damper
- General::d := 0
- force1
- General::animation := false
- General::resolveInFrame := resolveInFrame = Modelica.Mechanics.MultiBody.Types.ResolveInFrameB.world
- force
- General::animation := false
- General::resolveInFrame := resolveInFrame = Modelica.Mechanics.MultiBody.Types.ResolveInFrameB.world
- ramp_tgtAng
- General::height := 20
- General::duration := 1 [s]
- General::offset := 90
- General::startTime := 15 [s]
- revolute
- General::useAxisFlange := true
- General::phi.start := true, 60*Modelica.Constants.pi/180 [rad]
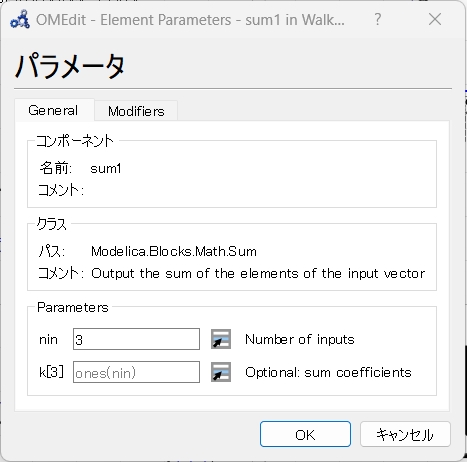
- sum1
- General::nin := 3
- trapezoid_distForce
- General::amplitude := 50
- General::rising := 0.001 [s]
- General::width := 0.02 [s]
- General::falling := 0.001 [s]
- General::period := 10 [s]
- General::nperiod := 1
- General::offset := 0
- General::startTime := 7 [s]
- world
- General::animateGravity := false
- General::animateGround := false


flange_bの位置(flange_aからの相対)を質量中心と設定する.
慣性モーメント、慣性積は与えず、(ゼロではなくデフォルトにしておく)、質量、慣性モーメントの無い棒とその先端に接続された質量を持つ球が振子を成すとする.(慣性モーメントは無しになるのではなく、flange_aからflange_bへのアームがそれを成す.)
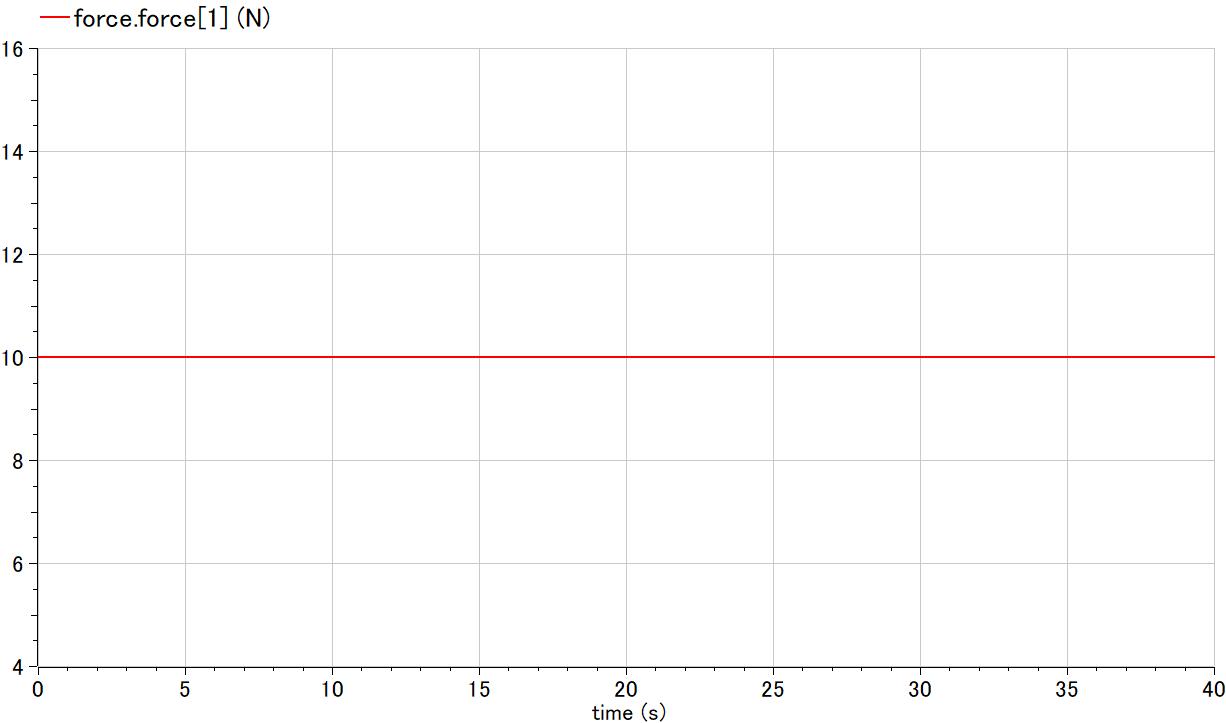
絶対座標からみてx方向に恒常力を与える.











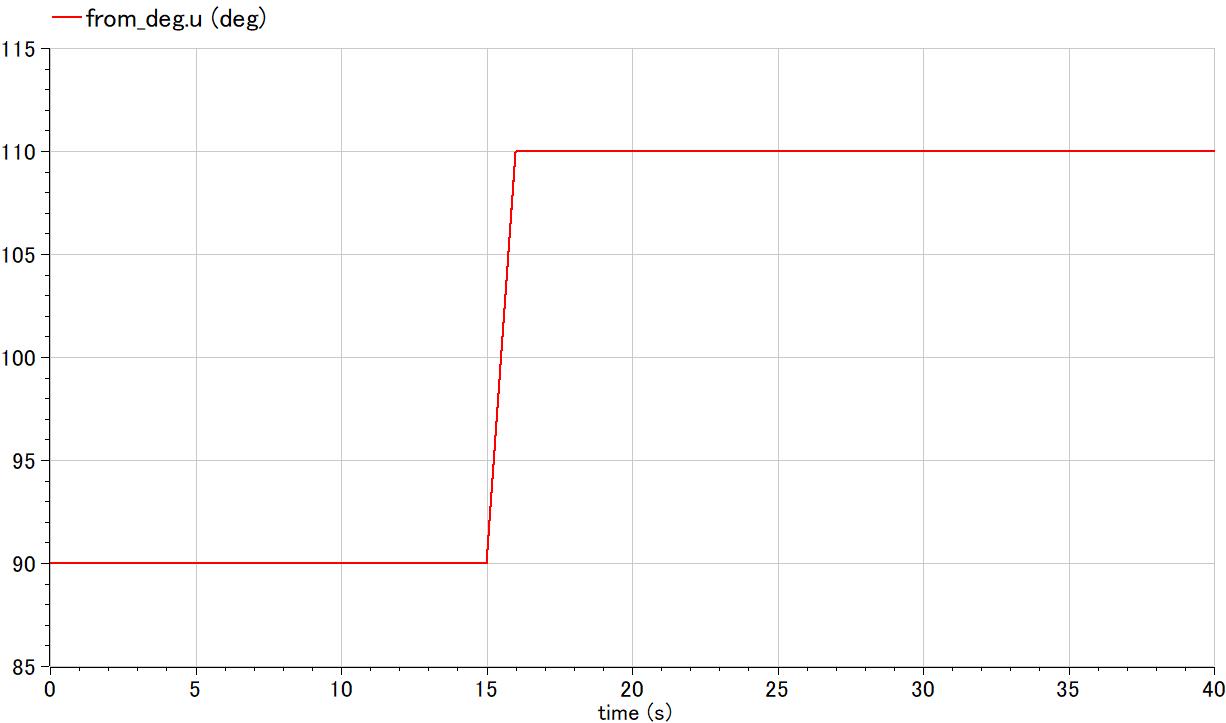
最初は直立状態を目標指示値とする.time=15[s]から、目標を20°増して斜めに傾いた位置で静定させる.

相対角度(flange_aから見たflange_bの角度)の初期値を与える.30°、直立から逸れた位置からスタートさせる.

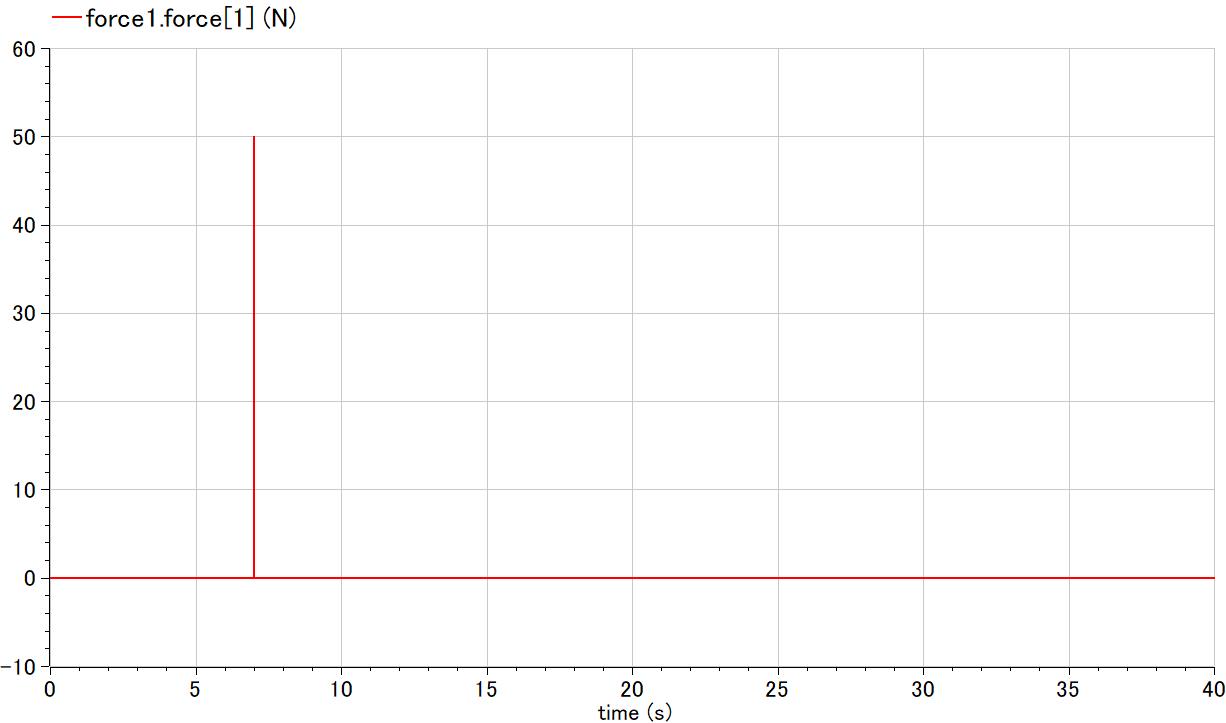
ハンマーで叩くような力の入力を与える.
rising, falling, widthに小さな値を与え、パルス状の入力信号にする.
台形波を周期的に与えられるコンポーネントだが、本例題では一回で良いので、nperiodに1を与える.

地面と重力の表示は本例題では邪魔なので非表示にする.
ソースコード
上記までを行うとOpenModelicaがソースコードを自動生成してくれている。エラーが生じた場合の比較のために、本モデルの完成状態のソースコードを示しておく。
完成状態のソースコード(チェック用)
コンパイルエラーや、計算結果が意図通りのものとならないような場合に比較・チェック用に参照して欲しい。尚、annotation()の部分はGUI上の配置位置や向きで値が変わるものなので、比較する必要は無い。
——————————————————————————-
model InvPend_CtrldTrq_001
extends Modelica.Icons.Example;
inner Modelica.Mechanics.MultiBody.World world(animateGravity = false, animateGround = false) annotation(
Placement(visible = true, transformation(origin = {-28, -76}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
Modelica.Mechanics.MultiBody.Joints.Revolute revolute(phi(displayUnit = "rad", fixed = true, start = 60*Modelica.Constants.pi/180), useAxisFlange = true) annotation(
Placement(visible = true, transformation(origin = {125, -59}, extent = {{-17, -17}, {17, 17}}, rotation = 90)));
Modelica.Mechanics.MultiBody.Parts.BodyShape bodyShape(angles_start = {0.5235987755982988, 0, 0}, length = bodyShape.r[1], m = 1, r = {0.6, 0, 0}, r_CM = bodyShape.r, sphereDiameter = 4^(1/3)*0.06, width = 1/8*bodyShape.sphereDiameter) annotation(
Placement(visible = true, transformation(origin = {125, 75}, extent = {{-17, -17}, {17, 17}}, rotation = 90)));
Modelica.Mechanics.Rotational.Components.Damper damper(d = 0, phi_nominal = 1e-9) annotation(
Placement(visible = true, transformation(origin = {84, -51}, extent = {{-8, -8}, {8, 8}}, rotation = 90)));
Modelica.Mechanics.Rotational.Sources.Torque torque_actuator annotation(
Placement(visible = true, transformation(origin = {52, -20}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
Modelica.Mechanics.Rotational.Sensors.RelAngleSensor relAngleSensor annotation(
Placement(visible = true, transformation(origin = {41, -45}, extent = {{-7, 7}, {7, -7}}, rotation = 90)));
Modelica.Blocks.Sources.Ramp ramp_tgtAng(duration = 1, height = 20, offset = 90, startTime = 15) annotation(
Placement(visible = true, transformation(origin = {-174, 24}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
Modelica.Blocks.Math.Feedback feedback annotation(
Placement(visible = true, transformation(origin = {-122, 24}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
Modelica.Blocks.Math.Gain ctrl_P(k = 30) annotation(
Placement(visible = true, transformation(origin = {-67, 24}, extent = {{-7, -7}, {7, 7}}, rotation = 0)));
Modelica.Blocks.Math.UnitConversions.From_deg from_deg annotation(
Placement(visible = true, transformation(origin = {-145, 24}, extent = {{-7, -7}, {7, 7}}, rotation = 0)));
Modelica.Blocks.Math.Sum sum1(nin = 3) annotation(
Placement(visible = true, transformation(origin = {-35, 24}, extent = {{-7, -7}, {7, 7}}, rotation = 0)));
Modelica.Blocks.Continuous.Integrator ctrl_I(k = 40) annotation(
Placement(visible = true, transformation(origin = {-67, -3}, extent = {{-7, -7}, {7, 7}}, rotation = 0)));
Modelica.Blocks.Continuous.Der der1 annotation(
Placement(visible = true, transformation(origin = {-89, -28}, extent = {{-7, -7}, {7, 7}}, rotation = 0)));
Modelica.Blocks.Math.Gain ctrl_D(k = 1) annotation(
Placement(visible = true, transformation(origin = {-67, -28}, extent = {{-7, -7}, {7, 7}}, rotation = 0)));
Modelica.Mechanics.MultiBody.Forces.WorldForce force1(animation = false, resolveInFrame = Modelica.Mechanics.MultiBody.Types.ResolveInFrameB.world) annotation(
Placement(visible = true, transformation(origin = {36, 92}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
Modelica.Blocks.Sources.Trapezoid trapezoid_distForce(amplitude = 50, falling = 0.001, nperiod = 1, offset = 0, period = 10, rising = 0.001, startTime = 7, width = 0.02) annotation(
Placement(visible = true, transformation(origin = {-84, 118}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
Modelica.Blocks.Sources.Constant const(k = 0) annotation(
Placement(visible = true, transformation(origin = {-81, 93}, extent = {{-5, -5}, {5, 5}}, rotation = 0)));
Modelica.Blocks.Sources.Constant const1(k = 0) annotation(
Placement(visible = true, transformation(origin = {-81, 77}, extent = {{-5, -5}, {5, 5}}, rotation = 0)));
Modelica.Mechanics.MultiBody.Forces.WorldForce force(animation = false, resolveInFrame = Modelica.Mechanics.MultiBody.Types.ResolveInFrameB.world) annotation(
Placement(visible = true, transformation(origin = {58, 168}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
Modelica.Blocks.Sources.Constant const2(k = 10) annotation(
Placement(visible = true, transformation(origin = {-65, 187}, extent = {{-9, -9}, {9, 9}}, rotation = 0)));
Modelica.Blocks.Sources.Constant const3(k = 0) annotation(
Placement(visible = true, transformation(origin = {-33, 177}, extent = {{-5, -5}, {5, 5}}, rotation = 0)));
Modelica.Blocks.Sources.Constant const4(k = 0) annotation(
Placement(visible = true, transformation(origin = {-33, 159}, extent = {{-5, -5}, {5, 5}}, rotation = 0)));
Modelica.Mechanics.MultiBody.Sensors.CutForce cutForce(animation = false, positiveSign = true, resolveInFrame = Modelica.Mechanics.MultiBody.Types.ResolveInFrameA.frame_resolve) annotation(
Placement(visible = true, transformation(origin = {78, 135}, extent = {{5, 5}, {-5, -5}}, rotation = -270)));
Modelica.Mechanics.MultiBody.Sensors.CutForce cutForce1(animation = false, positiveSign = true, resolveInFrame = Modelica.Mechanics.MultiBody.Types.ResolveInFrameA.frame_resolve) annotation(
Placement(visible = true, transformation(origin = {61, 92}, extent = {{-5, -5}, {5, 5}}, rotation = 0)));
Modelica.Mechanics.MultiBody.Sensors.CutForce cutForce_body_b_tot(animation = false, positiveSign = true, resolveInFrame = Modelica.Mechanics.MultiBody.Types.ResolveInFrameA.frame_resolve) annotation(
Placement(visible = true, transformation(origin = {93, 92}, extent = {{-5, -5}, {5, 5}}, rotation = 0)));
equation
connect(world.frame_b, revolute.frame_a) annotation(
Line(points = {{-18, -76}, {125, -76}}, thickness = 1));
connect(revolute.frame_b, bodyShape.frame_a) annotation(
Line(points = {{125, -42}, {125, 58}}, thickness = 2));
connect(revolute.support, damper.flange_a) annotation(
Line(points = {{108, -69}, {84, -69}, {84, -59}}, thickness = 1));
connect(damper.flange_b, revolute.axis) annotation(
Line(points = {{84, -43}, {98, -43}, {98, -59}, {108, -59}}, thickness = 1));
connect(relAngleSensor.flange_b, revolute.axis) annotation(
Line(points = {{41, -38}, {108, -38}, {108, -59}}, thickness = 0.5));
connect(revolute.support, relAngleSensor.flange_a) annotation(
Line(points = {{108, -69}, {41, -69}, {41, -52}}, thickness = 0.5));
connect(torque_actuator.flange, revolute.axis) annotation(
Line(points = {{62, -20}, {98, -20}, {98, -59}, {108, -59}}, thickness = 1));
connect(feedback.y, ctrl_P.u) annotation(
Line(points = {{-113, 24}, {-76, 24}}, color = {0, 0, 127}));
connect(relAngleSensor.phi_rel, feedback.u2) annotation(
Line(points = {{33, -45}, {-120, -45}, {-120, 16}, {-122, 16}}, color = {0, 0, 127}));
connect(from_deg.y, feedback.u1) annotation(
Line(points = {{-137.3, 24}, {-130.3, 24}}, color = {0, 0, 127}));
connect(ramp_tgtAng.y, from_deg.u) annotation(
Line(points = {{-163, 24}, {-155, 24}}, color = {0, 0, 127}));
connect(ctrl_P.y, sum1.u[1]) annotation(
Line(points = {{-59.3, 24}, {-42.3, 24}}, color = {0, 0, 127}));
connect(sum1.y, torque_actuator.tau) annotation(
Line(points = {{-27, 24}, {-18, 24}, {-18, -20}, {40, -20}}, color = {0, 0, 127}));
connect(ctrl_I.y, sum1.u[2]) annotation(
Line(points = {{-59.3, -3}, {-54.3, -3}, {-54.3, 24}, {-44.3, 24}}, color = {0, 0, 127}));
connect(feedback.y, ctrl_I.u) annotation(
Line(points = {{-113, 24}, {-103, 24}, {-103, -3}, {-76, -3}}, color = {0, 0, 127}));
connect(der1.y, ctrl_D.u) annotation(
Line(points = {{-81.3, -28}, {-75.3, -28}}, color = {0, 0, 127}));
connect(ctrl_D.y, sum1.u[3]) annotation(
Line(points = {{-59.3, -28}, {-49.3, -28}, {-49.3, 24}, {-43.3, 24}}, color = {0, 0, 127}));
connect(feedback.y, der1.u) annotation(
Line(points = {{-113, 24}, {-109, 24}, {-109, -28}, {-99, -28}}, color = {0, 0, 127}));
connect(trapezoid_distForce.y, force1.force[1]) annotation(
Line(points = {{-73, 118}, {-6.3, 118}, {-6.3, 92}, {24, 92}}, color = {0, 0, 127}, pattern = LinePattern.Dash));
connect(const.y, force1.force[2]) annotation(
Line(points = {{-75.5, 93}, {-10.9, 93}, {-10.9, 92}, {24, 92}}, color = {0, 0, 127}, pattern = LinePattern.Dash));
connect(const1.y, force1.force[3]) annotation(
Line(points = {{-75.5, 77}, {-16.4, 77}, {-16.4, 92}, {24, 92}}, color = {0, 0, 127}, pattern = LinePattern.Dash));
connect(force1.frame_resolve, world.frame_b) annotation(
Line(points = {{36, 82}, {6, 82}, {6, -76}, {-18, -76}}, pattern = LinePattern.Dash));
connect(const2.y, force.force[1]) annotation(
Line(points = {{-55, 187}, {18, 187}, {18, 168}, {46, 168}}, color = {0, 0, 127}, pattern = LinePattern.Dash));
connect(const3.y, force.force[2]) annotation(
Line(points = {{-27.5, 177}, {14, 177}, {14, 168}, {46, 168}}, color = {0, 0, 127}, pattern = LinePattern.Dash));
connect(const4.y, force.force[3]) annotation(
Line(points = {{-27.5, 159}, {-12, 159}, {-12, 168}, {46, 168}}, color = {0, 0, 127}, pattern = LinePattern.Dash));
connect(force.frame_resolve, world.frame_b) annotation(
Line(points = {{58, 158}, {6, 158}, {6, -76}, {-18, -76}}, color = {95, 95, 95}, pattern = LinePattern.Dash));
connect(force.frame_b, cutForce.frame_a) annotation(
Line(points = {{68, 168}, {78, 168}, {78, 140}}, color = {95, 95, 95}, thickness = 0.5));
connect(force1.frame_b, cutForce1.frame_a) annotation(
Line(points = {{46, 92}, {56, 92}}, color = {95, 95, 95}, thickness = 0.5));
connect(cutForce.frame_resolve, world.frame_b) annotation(
Line(points = {{73, 131}, {6, 131}, {6, -76}, {-18, -76}}, color = {95, 95, 95}, pattern = LinePattern.Dash));
connect(cutForce1.frame_resolve, world.frame_b) annotation(
Line(points = {{65, 87}, {65, 74}, {6, 74}, {6, -76}, {-18, -76}}, pattern = LinePattern.Dash));
connect(cutForce.frame_b, cutForce_body_b_tot.frame_a) annotation(
Line(points = {{78, 130}, {78, 92}, {88, 92}}, color = {95, 95, 95}, thickness = 0.5));
connect(cutForce1.frame_b, cutForce_body_b_tot.frame_a) annotation(
Line(points = {{66, 92}, {88, 92}}, color = {95, 95, 95}, thickness = 0.5));
connect(cutForce_body_b_tot.frame_b, bodyShape.frame_b) annotation(
Line(points = {{98, 92}, {126, 92}}, thickness = 0.5));
connect(world.frame_b, cutForce_body_b_tot.frame_resolve) annotation(
Line(points = {{-18, -76}, {6, -76}, {6, 74}, {97, 74}, {97, 87}}, pattern = LinePattern.Dash));
annotation(
experiment(StartTime = 0, StopTime = 40, Tolerance = 1e-09, Interval = 0.001),
Diagram(graphics = {Text(origin = {56, 0}, extent = {{-16, 6}, {16, -6}}, textString = "Positive
= clockwise", horizontalAlignment = TextAlignment.Left), Rectangle(origin = {-100, -1}, pattern = LinePattern.Dash, lineThickness = 0.5, extent = {{-96, 53}, {96, -53}}), Text(origin = {-162, 61}, extent = {{-28, 5}, {28, -5}}, textString = "control", horizontalAlignment = TextAlignment.Left), Text(origin = {48, 11}, extent = {{-34, 7}, {34, -7}}, textString = "Rotational Actuator", horizontalAlignment = TextAlignment.Left), Text(origin = {-92, 140}, extent = {{-48, 6}, {48, -6}}, textString = "Input Disturbance Force", horizontalAlignment = TextAlignment.Left), Text(origin = {-48, 206}, extent = {{-48, 6}, {48, -6}}, textString = "Constant disturbance force", horizontalAlignment = TextAlignment.Left), Text(origin = {-166, -9}, extent = {{-26, 13}, {26, -13}}, textString = "Input signal:
target angle", horizontalAlignment = TextAlignment.Left)}, coordinateSystem(extent = {{-200, -100}, {160, 220}})));
end InvPend_CtrldTrq_001;
——————————————————————————-
シミュレーション実行&結果評価
- relAngleSensor.phi_rel
- torque_actuator.tau
- ctrls
それでは、観たいvariableの値や動きを評価してゆこう。
本連載はOpenModelicaでモデルを組む演習が主目的なのでサクサク観てゆく。本記事では答え合わせとして軽い解説で進めるが、実用としてModelica,1DCAEを実物/試験を再現したり、設計予測に使えるようになったら、本来はこの段階の考察が最も重要かつ時間をかけるべきところだ。その点は憶えておいて頂きたい。
Setup
今回はOpenModelicaの結果をアニメーション表示する機能を使う.そのため、普段は触っていない(特にFluid)項目の設定を触る.
下図に示すように、「全般」タブの一番下にある「Launch Animation」にチェックを入れる.これを行わないとシミュレーション実行完了後にアニメーション表示が出ない.なお、ここで(コンパイル&実行の段階)で設定し損じていても、plot viewで、再シミュレーション実行でコンパイルを飛ばして再実行すれば、その際に設定する事は可能.
Input確認
意図通りの操作を与えられているか・反映されているかを,rampのoutout connector以外のvariableで確認する.
Output
アニメーション表示
時系列グラフで見るより、アニメーション表示を見た方が圧倒的に理解しやすいので、まずはそれを見よう.animationに簡易な解説字幕を付した動画を公開しているので、結果の確認に参照して欲しい.
plot
振子の角度.
最初に、60[deg]という、静定目標位置から開始して、風による恒常力入力を受けている中でも無事に90[deg]直立状態に向かって動き、減衰して静定してゆく.
time=7[s]にてパルス外乱を与えてもその挙動は変わらず、一度直列状態から離れるが、直ぐに直立位置へと戻ってくる.
time=15[s]から指示角度を110[deg](直立から20[deg]傾いた状態)へと変更しても、軽いオーバーシュートは起こすが短時間で減衰し、110[deg]で静定する.
この時間応答は、P,I,Dそれぞれの制御ゲインによって大きく異なる.是非デフォルトのものから変更してシミュレーションを実行してみて、どのような挙動になるかを見て欲しい.(*後日、本モデルを用いてPID制御項のパラメータを、制御対象の挙動が意図したものになるようにチューニングする講座の記事も作成しようと考えている.)
.jpg?raw=true)
トルクアクチュエータが発生するトルク.振子のヒンジへの入力.
参考で確認するのみであるが、静定時にトルクが0ではない事には注目しておいて欲しい.恒常外力入力が有る事と、支持角度変更後は支えが無ければ重力で落下してしまうのを強制的に支えているためである.
シミュレーションから実物の機器を設計する場合は、この結果が必要なモータトルクを意味しており、少なくともここで得た結果より大きなトルクを発生させられるモータを用意しなければならない事になる(逆にトルク出力の最小分解能も).

ctrl_P.y, ctrl_I.y, ctrl_D.y
P制御器、I制御器、D制御器それぞれの出力信号.参考情報.
簡単に見ると、Iが外力に対抗して目標位置に向かうために出力を発し、P、Dがダンパ付きバネのように中立位置へ戻ろうとする弾性と振動を弱める減衰の役割を果たしているのが読み取れるかと思う.

最後に
Multibody libraryを用いた(+1D rotation libraryを組み合わせた)初歩的な機構モデリングを学んだ.
また、Blocks libraryを用いてPID制御を組み込み、物理的に動く物体を能動的に制御する例に取り組んだ.
非常にシンプルかつ初歩的例題だが、モデリングと背景理論としては多くのエッセンスを内包したものである.parameterを変えてsimulationを実施するだけでも勉強になると考えられるので、是非作成したモデルで遊んで貰いたい.
本例題は以上。
例モデルに関する情報
本記事で取り上げたモデルは専用の「WalkingInWorldOfMechatronics」ライブラリに公開しており、その情報を記しておく。ソースコードは本記事にも記載したが、直接OpenModelicaで読み込みたい方はダウンロードしてGPL3の範囲内で自由に使っていただいて構わない。
- モデルのフルパス:WalkingInWorldOfMechatronics.Easy.InvPend_CtrldTrq_001
- githubのライブラリページリンク
以上




コメント